Вычисление произведения векторов является важной задачей в линейной алгебре. Произведение трех векторов по координатам позволяет найти новый вектор, который является результатом их взаимодействия. Этот процесс часто используется в физике, механике и других областях науки.
Чтобы найти произведение трех векторов по координатам, необходимо знать координаты каждого вектора. Обозначим эти векторы как A, B и C. Произведение трех векторов определяется следующей формулой:
(A x B) x C = A x (B x C)
Здесь символ "x" обозначает векторное произведение. Для вычисления векторного произведения двух векторов можно использовать формулу:
(A x B) = (A2 * B3 - A3 * B2)i + (A3 * B1 - A1 * B3)j + (A1 * B2 - A2 * B1)k
Где A1, A2, A3, B1, B2, B3 - координаты векторов A и B. Индексы i, j и k обозначают координаты нового вектора.
Таким образом, зная координаты трех векторов, вы можете вычислить их произведение и получить новый вектор. Векторное произведение трех векторов по координатам является мощным инструментом и находит свое применение в различных областях науки и инженерии.
Методика вычисления произведения трех векторов

1. Запишите координаты трех векторов в виде матрицы, где каждый вектор является строкой:
| Вектор 1 | Вектор 2 | Вектор 3 |
|---|---|---|
| x1 | y1 | z1 |
| x2 | y2 | z2 |
| x3 | y3 | z3 |
2. Вычислите определитель этой матрицы и получите значение произведения трех векторов:
P = | x1 y1 z1 |
| x2 y2 z2 | = x1*y2*z3 + y1*z2*x3 + z1*x2*y3 - z1*y2*x3 - y1*x2*z3 - x1*z2*y3
Таким образом, произведение трех векторов может быть легко вычислено с использованием указанной методики. Оно позволяет определить зависимость и взаимное расположение трех векторов и является полезным инструментом при решении различных задач в линейной алгебре.
Вводные сведения о трехмерных векторах
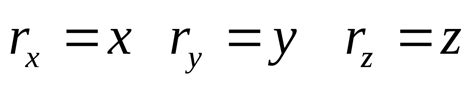
Трехмерные векторы состоят из трех компонентов, которые обозначаются в виде (x, y, z), где x, y и z являются координатами вектора по осям x, y и z соответственно. Векторы могут использоваться для представления физических величин, таких как сила, скорость или сила тяжести, а также для решения различных математических задач.
Произведение трех векторов, известное также как смешанное произведение, является важным понятием в линейной алгебре. Он позволяет вычислить объем параллелепипеда, построенного на трех векторах. Для вычисления смешанного произведения трех векторов необходимо перемножить их координаты и применить определенную формулу.
| Компоненты вектора | Обозначение |
| x-координата | x |
| y-координата | y |
| z-координата | z |
Трехмерные векторы имеют множество применений в физике, геометрии, компьютерной графике и других областях. Наличие трех компонентов позволяет точно описывать направление и величину вектора, что делает их удобными инструментами для моделирования и анализа трехмерных объектов.
Как представить векторы по координатам

Для представления векторов по координатам нам необходимо знать его длину и направление. Координаты вектора могут быть представлены в виде упорядоченной пары чисел, где каждое число соответствует координате вектора в определенной системе координат.
Существует несколько способов задания векторов по координатам:
- Канонический способ. В этом способе координаты вектора записываются в виде упорядоченной пары чисел в квадратных скобках, например [x, y]. Где x - координата вектора по оси X, а y - координата вектора по оси Y.
- Декартов способ. В этом способе координаты вектора записываются в виде упорядоченной пары чисел в скобках через запятую, например (x, y).
- Компонентный способ. В этом способе координаты вектора записываются в виде отдельных чисел, разделенных запятой, например x, y.
Необходимо помнить, что порядок координат важен и определяет направление вектора. Также важно выбрать правильную систему координат, чтобы корректно задать координаты вектора.
Арифметические операции над векторами

Векторами называют упорядоченные наборы чисел, которые представляют собой направление и величину физической величины. Векторы могут быть представлены в виде списка чисел, называемых компонентами вектора, или в виде геометрических объектов, имеющих направление и длину.
Для векторов определены основные арифметические операции:
Сложение векторов: при сложении векторов их соответствующие компоненты складываются поэлементно. Например, для векторов AB = (a1, a2, a3) и CD = (b1, b2, b3), их сумма будет равна AB + CD = (a1 + b1, a2 + b2, a3 + b3).
Вычитание векторов: при вычитании векторов из первого вектора вычитаются соответствующие компоненты второго вектора. Например, для векторов AB = (a1, a2, a3) и CD = (b1, b2, b3), их разность будет равна AB - CD = (a1 - b1, a2 - b2, a3 - b3).
Умножение вектора на скаляр: при умножении вектора на число все его компоненты умножаются на это число. Например, для вектора AB = (a1, a2, a3) и числа k, результатом будет k * AB = (k * a1, k * a2, k * a3).
Умножение векторов: векторное произведение двух векторов определяется как вектор, перпендикулярный плоскости, образованной этими векторами, и его длина равна произведению длин исходных векторов на синус угла между ними. Например, для векторов AB = (a1, a2, a3) и CD = (b1, b2, b3), их векторное произведение будет равно AB x CD = ((a2 * b3 - a3 * b2), (a3 * b1 - a1 * b3), (a1 * b2 - a2 * b1)).
Арифметические операции над векторами позволяют выполнять различные математические действия и решать задачи в различных областях, таких как физика, геометрия и программирование.
Поиск произведения трех векторов по координатам

Для того чтобы найти произведение трех векторов по их координатам, следует применить правило векторного произведения. Векторное произведение двух векторов вычисляется с помощью определителя третьего порядка.
Дано три вектора: A (a₁, a₂, a₃), B (b₁, b₂, b₃) и C (c₁, c₂, c₃). При вычислении произведения трех векторов A × B × C сначала находим векторное произведение первых двух векторов A × B, а затем векторно умножаем полученный вектор на третий вектор C по правилу:
A × B × C = (A × B) × C
После найденного векторного произведения (A × B) умножаем на третий вектор C по формуле:
(A × B) × C = (a₂b₃ - a₃b₂, a₃b₁ - a₁b₃, a₁b₂ - a₂b₁) × C
Результатом будет новый вектор, полученный в результате произведения трех исходных векторов.