При изучении математики, одной из самых важных частей является нахождение производных функций. Иногда возникают ситуации, когда необходимо найти производную числа, возведенного в степень сложной функции.
Для того чтобы найти производную такого числа, необходимо применить правило дифференцирования, которое устанавливает, что производная числа, возведенного в степень сложной функции, равна производной самой функции, умноженной на логарифм числа.
То есть, если имеется число a, возведенное в степень сложной функции f(x), то его производная будет равна f'(x) * log(a).
Такое правило является очень полезным при решении математических задач, где требуется находить производные сложных выражений. Например, при решении задач по оптимизации функций, при нахождении нулей функций и т.д.
Производная и ее значение
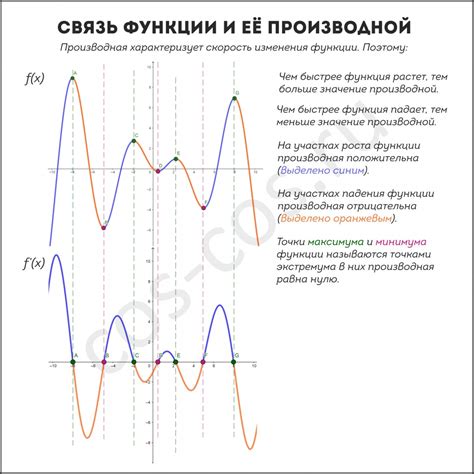
Значение производной в конкретной точке может дать важную информацию о свойствах функции. Она может помочь определить экстремумы функции (максимумы и минимумы), места перегиба, а также позволяет построить график функции. В контексте возведения числа в степень сложной функции, производная позволяет найти скорость изменения значения числа в зависимости от изменения ее аргумента.
| Обозначение | Описание |
|---|---|
| f'(x) | Производная функции f(x) |
| x | Аргумент функции |
| y | Значение функции для аргумента x |
| dy/dx | Значение производной y по x |
Производная числа при возведении в степень сложной функции вычисляется с использованием цепного правила дифференцирования. Оно позволяет разложить производную сложной функции на произведение производных простых функций. Зная производные простых функций, можно выразить производную сложной функции через производные ее составляющих.
Производная и ее значение являются важными понятиями в математике. Они позволяют анализировать функции, устанавливать свойства графиков, исследовать темпы изменения и оптимизировать процессы. Понимание производной и ее значения помогает более глубоко понять и использовать математические методы в различных областях науки и техники.
Возведение числа в степень

В общем виде возведение числа в положительную степень выглядит следующим образом:
| a0 | = | 1 |
| a1 | = | a |
| a2 | = | a * a |
| a3 | = | a * a * a |
| ... | ... | ... |
| an | = | a * a * a * ... * a (n раз) |
При возведении числа в отрицательную степень, необходимо взять обратное значение числа в положительной степени. Так, например, a-n = 1 / an.
Также стоит отметить, что возведение числа в дробную степень аналогично вычислению корня. Например, a1/2 = √a.
Некоторые особые случаи возведения числа в степень:
- Возведение числа в нулевую степень всегда равно 1.
- Возведение нуля в любую степень (кроме нуля) всегда равно 0.
Сложная функция

f'(g(x)) * g'(x)
То есть, сначала находим производную внешней функции f'(g(x)), а затем умножаем производную внутренней функции g'(x).
Процесс нахождения производной сложной функции требует использования цепного правила, а также знание производных элементарных функций. Здесь важно уметь правильно разбить функцию на внешнюю и внутреннюю, чтобы применить соответствующее правило дифференцирования.
Пример:
Дана функция f(x) = (2x + 1)^3. Необходимо найти производную этой функции.
Решение:
В данном случае функция g(x) = 2x + 1 является внутренней функцией, а функция f(x) = g(x)^3 - внешней. Применяем цепное правило и находим производные:
f'(x) = 3(g(x))^2 * g'(x) = 3(2x + 1)^2 * 2 = 6(2x + 1)^2
Таким образом, производная функции f(x) = (2x + 1)^3 равна 6(2x + 1)^2.
Производная сложной функции

Если дана функция f(x), которая является сложной функцией g(h(x)), то для нахождения ее производной необходимо применить правило сложной функции. Сначала необходимо найти производную внешней функции g(h(x)), а затем умножить ее на производную внутренней функции h(x).
Процесс нахождения производной сложной функции можно проиллюстрировать с помощью таблицы:
| Внешняя функция g | Внутренняя функция h | Производная внешней функции g' | Производная внутренней функции h' | Производная сложной функции f'(x) |
|---|---|---|---|---|
| g(x) = sin(x) | h(x) = x^2 | g'(x) = cos(x) | h'(x) = 2x | f'(x) = g'(h(x)) * h'(x) = cos(h(x)) * 2x |
| g(x) = e^x | h(x) = ln(x) | g'(x) = e^x | h'(x) = 1/x | f'(x) = g'(h(x)) * h'(x) = e^ln(x) * 1/x = x/x = 1 |
Таким образом, для нахождения производной сложной функции необходимо найти производные внешней и внутренней функций, а затем умножить их друг на друга. Таблица позволяет наглядно представить этот процесс и помогает в решении подобных задач.
Производная числа при возведении в степень

Для нахождения производной числа при возведении в степень необходимо использовать основное свойство степенной функции. Если имеется функция вида f(x) = ab(x), где a и b(x) – функции, а x – независимая переменная, то производная этой функции будет равна:
f'(x) = (ab(x))'(x) = ab(x) * ln(a) * b'(x)
где ln(a) – натуральный логарифм числа a, а b'(x) – производная функции b(x) по x.
Таким образом, нахождение производной числа при возведении в степень сводится к умножению и сложению. Зная значения a и b(x), а также производную функции b'(x), можно легко найти значение производной числа при возведении в степень.
Пример:
Дано числовое выражение f(x) = 23x. Чтобы найти производную этого числа при возведении в степень, необходимо применить формулу: f'(x) = (23x)'(x) = 23x * ln(2) * (3x)'.
Далее необходимо найти производную функции b(x) = 3x, используя правило дифференцирования произведения: (3x)' = 3 * 1 = 3. Подставляем полученные значения в формулу, и получаем: f'(x) = 23x * ln(2) * 3 = 63x * ln(2).
Таким образом, производная числа при возведении в степень равна 63x * ln(2). Это значение позволяет нам узнать скорость изменения числа при изменении значения x.
Практический пример вычисления производной числа при возведении в степень сложной функции

Пусть у нас имеется функция f(x), заданная выражением:
f(x) = (3x + 2)²
Нам необходимо найти производную числа a при его возведении в степень f(x).
Для решения этой задачи потребуется использовать свойство произведения и степени:
Если A - функция, а n - число, то производная числа n при его возведении в степень A равна:
| Формула | Численное значение |
|---|---|
| (n^A)' = A * n^(A-1) | (a^f(x))' = f(x) * a^(f(x)-1) |
Подставим значения функции f(x) и производной f'(x) в данную формулу:
(3x + 2)² = f(x)
f'(x) = (3x + 2)² * a^((3x + 2)² - 1)
Таким образом, мы получили выражение для производной числа a при его возведении в степень f(x).
Данная формула позволяет нам вычислить производную числа при возведении в степень сложной функции и решить различные задачи, связанные с этим. Используя данную формулу в сочетании с другими правилами дифференцирования, можно найти производные более сложных функций и применить их в решении реальных задач.