Нахождение производной является одной из фундаментальных задач математического анализа. Оно позволяет найти скорость изменения функции в каждой точке области определения. В свою очередь, числа в степени квадратного уравнения представляют собой специальный случай функции, которая имеет вид \(f(x) = ax^2 + bx + c\), где \(a\), \(b\) и \(c\) - это коэффициенты этого уравнения.
Для нахождения производной таких чисел, существует простая и понятная инструкция. Сначала нужно продифференцировать каждый член уравнения. Так как производная константы равна нулю, то последний член \(c\) дифференцированию не подлежит. Затем нужно применить правило показателя степени для дифференцирования каждого монома. Полученные производные складываются и дают окончательный результат - производную этого квадратного уравнения.
Для лучшего понимания процесса нахождения производной чисел в степени квадратного уравнения, рассмотрим несколько полезных примеров. Пусть у нас есть уравнение \(y = 2x^2 + 3x + 1\). Чтобы найти производную этого уравнения, нужно продифференцировать каждый из его членов. Таким образом, производная первого члена будет равна \(4x\), производная второго члена - \(3\), а производная последнего члена - ноль.
Методы нахождения производной квадратного уравнения
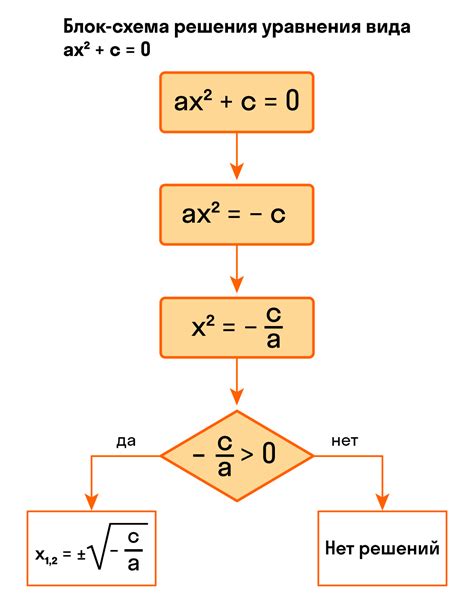
- Метод дифференцирования по определению: Для нахождения производной квадратного уравнения сначала необходимо разложить его на множители. Затем применяется правило дифференцирования по определению для каждого множителя. Например, для квадратного уравнения вида f(x) = (x - a)(x - b) можно использовать следующие шаги:
- Разложить уравнение на множители: f(x) = x^2 - (a + b)x + ab.
- Дифференцировать каждый множитель: f'(x) = 2x - (a + b).
- Разложить уравнение на составные части: f(x) = (x - a)^2.
- Дифференцировать каждую часть: g(x) = x^2, h(x) = x - a.
- Применить правило дифференцирования сложной функции: f'(x) = g'(h(x)) * h'(x) = 2(x - a) * 1 = 2(x - a).
Методы нахождения производной квадратного уравнения могут быть использованы для решения различных математических задач и построения графиков функций.
Пример нахождения производной числа в степени квадратного уравнения
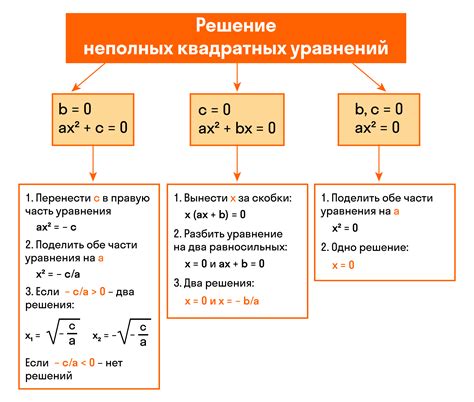
Рассмотрим пример нахождения производной числа в степени квадратного уравнения, чтобы лучше понять этот процесс. Пусть дано уравнение:
y = (2x^2 + 3x + 1)^3
Для начала нам необходимо раскрыть скобку, используя степень:
y = (8x^6 + 36x^5 + 54x^4 + 36x^3 + 9x^2 + 6x + 1)
Теперь мы можем найти производную данного уравнения. Для этого нужно взять производную от каждого слагаемого и перемножить его на производную степени. Найдем производную каждого слагаемого:
| Слагаемое | Производная слагаемого | Производная степени | Произведение |
|---|---|---|---|
| 8x^6 | 48x^5 | 3(2x^2 + 3x + 1)^2 | 144x^5(2x^2 + 3x + 1)^2 |
| 36x^5 | 180x^4 | 3(2x^2 + 3x + 1)^2 | 540x^4(2x^2 + 3x + 1)^2 |
| 54x^4 | 216x^3 | 3(2x^2 + 3x + 1)^2 | 648x^3(2x^2 + 3x + 1)^2 |
| 36x^3 | 108x^2 | 3(2x^2 + 3x + 1)^2 | 324x^2(2x^2 + 3x + 1)^2 |
| 9x^2 | 18x | 3(2x^2 + 3x + 1)^2 | 54x(2x^2 + 3x + 1)^2 |
| 6x | 6 | 3(2x^2 + 3x + 1)^2 | 18(2x^2 + 3x + 1)^2 |
| 1 | 0 | 3(2x^2 + 3x + 1)^2 | 3(2x^2 + 3x + 1)^2 |
Теперь соединим все произведения и получим:
y' = 144x^5(2x^2 + 3x + 1)^2 + 540x^4(2x^2 + 3x + 1)^2 + 648x^3(2x^2 + 3x + 1)^2 + 324x^2(2x^2 + 3x + 1)^2 + 54x(2x^2 + 3x + 1)^2 + 18(2x^2 + 3x + 1)^2 + 3(2x^2 + 3x + 1)^2
Таким образом, мы нашли производную числа в степени квадратного уравнения. Этот пример демонстрирует, как использовать степень и правило производной для нахождения производной сложной функции.
Применение производной числа в степени квадратного уравнения в реальной жизни
Производная числа в степени квадратного уравнения имеет широкое применение в различных областях реальной жизни. Ниже приведены некоторые примеры использования производной числа в степени квадратного уравнения:
| Область применения | Пример |
|---|---|
| Физика | При расчете движения тела в пространстве производная числа в степени квадратного уравнения используется для определения скорости и ускорения объекта. |
| Финансы | При анализе финансовых рынков производная числа в степени квадратного уравнения может использоваться для прогнозирования изменений цен на акции и определения оптимальных временных интервалов для покупки или продажи акций. |
| Инженерия | В инженерных расчетах производная числа в степени квадратного уравнения может применяться для определения оптимальных параметров конструкции, например, при проектировании мостов или зданий. |
| Медицина | Дифференцирование числа в степени квадратного уравнения может применяться для анализа медицинских данных, например, для определения изменения показателей здоровья пациента во времени. |
Таким образом, производная числа в степени квадратного уравнения является мощным инструментом, который находит свое применение в различных областях науки и практической деятельности.