Производная дроби с иксом в числителе и знаменателе – это одна из основных задач в математике, с которой сталкиваются ученики и студенты на разных уровнях обучения. На первый взгляд, эта задача может показаться сложной и неочевидной, однако с правильным подходом и знанием основных правил дифференцирования, она может быть решена сравнительно легко и с минимальными усилиями.
Для начала, важно вспомнить основное правило дифференцирования, согласно которому производная некоторой функции равна производной ее числителя, умноженной на знаменатель, минус производная знаменателя, умноженного на числитель, все это делено на квадрат знаменателя. Давайте рассмотрим пример, чтобы лучше понять, как это работает.
Предположим, у нас есть функция f(x) = (x + 1) / (x - 2), и мы хотим найти ее производную. В этом случае, числитель функции равен x + 1, а знаменатель равен x - 2. Применяя описанное ранее правило, мы можем записать производную f'(x) следующим образом:
Почему важно знать, как найти производную дроби с иксом в числителе и знаменателе?
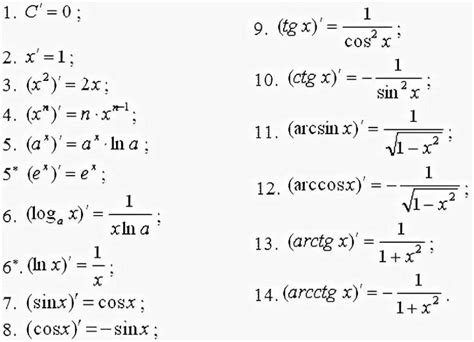
Одной из часто встречающихся формул в математике является дробь, где в числителе и знаменателе присутствуют переменные, включая переменную икс. Нахождение производной таких дробей позволяет нам анализировать их поведение и прогнозировать значения в различных точках.
Умение находить производную дробей с иксом в числителе и знаменателе является важным инструментом для решения различных задач. Например, при моделировании физических явлений, математическом анализе экономических данных или оптимизации процессов в инженерии.
Знание производных дробей не только помогает точнее описывать и предсказывать различные явления, но и позволяет эффективно решать математические задачи. Нахождение производной дроби с иксом в числителе и знаменателе позволяет сокращать дроби, приводить к общему знаменателю и упрощать алгебраические выражения, что экономит время и упрощает дальнейшие математические операции.
Таким образом, знание и умение находить производные дробей с иксом в числителе и знаменателе является неотъемлемой частью математического анализа и имеет широкое практическое применение. Понимание производных дробей позволяет более глубоко изучать и анализировать различные явления, моделировать их на компьютере и принимать обоснованные решения на основе полученных данных.
Приложения производной дроби с иксом в числителе и знаменателе

Производная дроби, в которой икс находится как в числителе, так и в знаменателе, встречается во многих математических задачах и приложениях. Определение и вычисление производной такой дроби может быть полезно в различных научных и инженерных областях, а также в физических и экономических моделях.
Приложения производной дроби с иксом в числителе и знаменателе можно обнаружить в некоторых физических законах и явлениях. Например, в законе Гука, который описывает связь между силой, действующей на упругую пружину, и ее деформацией. Если величину силы и деформации пружины представить в виде дроби с иксом в числителе и знаменателе, то производная такой дроби будет показывать, насколько быстро меняется сила или деформация при изменении икса.
Другим примером приложения производной дроби с иксом в числителе и знаменателе может быть экономическая модель, описывающая зависимость объема продаж товара от его цены. Если цену и объем продаж представить в виде дроби с иксом в числителе и знаменателе, то производная такой дроби будет показывать, насколько быстро меняется объем продаж при изменении цены.
В общем случае, производная дроби с иксом в числителе и знаменателе может быть полезна для анализа и оптимизации математических моделей, в которых икс представляет некоторую переменную, а числитель и знаменатель задают зависимость этой переменной от других факторов. Приложения таких моделей могут включать в себя дифференциальные уравнения, оптимизацию функций и моделирование различных физических и экономических процессов.
Таким образом, понимание и использование производной дроби с иксом в числителе и знаменателе является важным инструментом во многих научных и практических областях, где требуется анализ и оптимизация зависимостей между переменными и факторами.
Советы по нахождению производной дроби с иксом в числителе и знаменателе

Нахождение производной дроби с переменной x в числителе и знаменателе может показаться сложной задачей, но с помощью нескольких простых правил можно справиться с ней. Вот несколько советов, которые помогут вам находить производные таких дробей.
- Прежде всего, разделяйте задачу на две части: нахождение производной числителя и знаменателя отдельно, а затем применение правила деления производных.
- Для нахождения производной числителя используйте правило дифференцирования степенной функции: если числитель имеет вид x^n (где n - степень), то производная равна n*x^(n-1). Например, производная от x^2 будет равна 2*x^(2-1) = 2x.
- Аналогично, для нахождения производной знаменателя применяйте те же правила дифференцирования степенной функции.
- После нахождения производных числителя и знаменателя, примените правило деления производных: производная дроби равна (производная числителя * знаменатель - числитель * производная знаменателя) / знаменатель^2.
- Не забывайте упрощать полученное выражение, если это необходимо.
Пример: для нахождения производной дроби (x^2 + 1) / (x + 2) сначала находим производные числителя и знаменателя: производная числителя будет равна 2x, а производная знаменателя будет равна 1. Затем, применяя правило деления производных, получаем производную дроби: (2x*(x + 2) - (x^2 + 1)*1) / (x + 2)^2. Данное выражение можно дальше упростить, если это необходимо.
Таким образом, следуя данным советам, вы сможете находить производные дробей с переменной x в числителе и знаменателе. Помните, что практика и упражнения помогут вам освоить данную тему и повысить свои навыки в дифференцировании.
Изучите правила дифференцирования дробей с иксом в числителе и знаменателе

Существует несколько основных правил, которые следует помнить при дифференцировании дробей с иксом:
| Правило | Пример |
|---|---|
| Правило Лейбница | (u/v)' = (u'v - uv') / v^2, где u и v - функции от x |
| Правило деления | (1/v)' = - v' / v^2, где v - функция от x |
| Правило умножения | (uv)' = u'v + uv', где u и v - функции от x |
| Правило сложения | (u + v)' = u' + v', где u и v - функции от x |
| Правило вычитания | (u - v)' = u' - v', где u и v - функции от x |
Правило Лейбница является основным для дифференцирования дробей, и его использование особенно полезно, если числитель и знаменатель содержат переменную x в разных степенях или если в числителе или знаменателе присутствуют сложные функции.
Применение этих правил требует понимания основ дифференциального исчисления и знания правил арифметики. Поэтому перед тем, как приступить к дифференцированию дробей, рекомендуется полностью разобраться с этими правилами и пройти соответствующие математические курсы.
Используйте правило Лейбница для производной дроби с иксом в числителе и знаменателе

При нахождении производной дроби, в которой в числителе и знаменателе присутствует переменная x, можно воспользоваться правилом Лейбница. Это правило позволяет найти производную сложной функции.
Правило Лейбница гласит:
Если у нас есть функция F(x) = g(x) / h(x), где g(x) и h(x) - функции, зависящие от переменной x, то производная этой функции будет равна:
F'(x) = (g'(x) * h(x) - g(x) * h'(x)) / h(x)^2.
При применении правила Лейбница необходимо найти производные функций g(x) и h(x) по отдельности и подставить их в формулу. Затем выполнить алгебраические операции по упрощению выражения.
Давайте рассмотрим пример. Пусть у нас есть функция F(x) = (3x^2 + 2x + 1) / (x^2 - 4).
Сначала найдем производные функций в числителе и знаменателе:
g'(x) = 6x + 2,
h'(x) = 2x.
Теперь подставим эти значения в формулу:
F'(x) = ((6x + 2) * (x^2 - 4) - (3x^2 + 2x + 1) * 2x) / (x^2 - 4)^2.
После выполнения алгебраических операций мы получим окончательное выражение для производной функции F(x).
Примеры нахождения производной дроби с иксом в числителе и знаменателе

Найдем производную для следующей дроби:
y = (2x + 3) / (x^2 + 1)
Для начала раскроем скобки в числителе:
y = (2x + 3) / (x^2 + 1) = 2x / (x^2 + 1) + 3 / (x^2 + 1)
Затем обозначим эти два слагаемых как u и v соответственно:
u = 2x / (x^2 + 1)
v = 3 / (x^2 + 1)
Далее найдем производные слагаемых:
du/dx = (2(x^2 + 1) - 2x(2x)) / (x^2 + 1)^2 = (2x^2 + 2 - 4x^2) / (x^2 + 1)^2 = (-2x^2 + 2) / (x^2 + 1)^2
dv/dx = 0 - (3(2x)) / (x^2 + 1)^2 = -6x / (x^2 + 1)^2
Используя правило дифференцирования частного функций, получаем:
dy/dx = (u * dv/dx - v * du/dx) / (v^2) = ((2x / (x^2 + 1)) * (-6x / (x^2 + 1)^2) - (3 / (x^2 + 1)) * (-2x^2 + 2) / (x^2 + 1)^2) / ((3 / (x^2 + 1))^2)
Упростим полученное выражение, умножив числитель и знаменатель на (x^2 + 1)^2:
dy/dx = (2x * (-6x) - (3 * (-2x^2 + 2))) / (x^2 + 1) / ((3)^2)
Далее можно упростить числитель путем раскрытия скобок и сократить выражения:
dy/dx = (-12x^2 + 12 + 6x^2 - 6) / (9 * (x^2 + 1))
Сократив выражения получим окончательный ответ:
dy/dx = (-6x^2 + 6) / (9 * (x^2 + 1))
Таким образом, производная исходной дроби равна (-6x^2 + 6) / (9 * (x^2 + 1)).
Пример 1: Найти производную дроби с иксом в числителе и знаменателе

Давайте рассмотрим пример: найти производную функции f(x) = (2x + 1) / (3x - 2). Для начала, мы можем использовать правило дифференцирования, которое гласит, что производная функции a(x) / b(x) равна (a'(x)b(x) - a(x)b'(x)) / (b^2(x)).
Применяем это правило к нашей функции:
- Вычисляем производные числителя и знаменателя:
- a'(x) = 2
- b'(x) = 3
- Подставляем производные в формулу:
- (2 * (3x - 2) - (2x + 1) * 3) / ((3x - 2)^2)
- Выполняем вычисления:
- (6x - 4 - 6x - 3) / ((3x - 2)^2)
- (-7) / ((3x - 2)^2)
Таким образом, производная функции f(x) равна -7 / ((3x - 2)^2). Это и есть результат.
Приведенный пример демонстрирует, как найти производную дроби с иксом в числителе и знаменателе. Этот метод можно применять к любому аналогичному типу функций. Важно помнить о правиле дифференцирования дроби и упрощать полученное выражение, если это возможно.
Пример 2: Применение правил дифференцирования к дроби с иксом в числителе и знаменателе

Для наглядности рассмотрим пример дифференцирования дроби с иксом в числителе и знаменателе:
Пусть дана функция f(x) = (x^2 + 2x + 1) / (x^2 + x).
Мы хотим найти производную этой функции f'(x).
Применим правило дифференцирования для дроби:
| f'(x) = | [ (x^2 + x) * (2x + 2) - (x^2 + 2x + 1) * (2x + 1) ] / (x^2 + x)^2 |
| (2x^3 + 2x^2 + 2x^2 + 2x - 2x^3 - 2x^2 - 2x - x^2 - 2x - 1) / (x^2 + x)^2 | |
| (x^2 - 1) / (x^2 + x)^2 |
Таким образом, производная функции f(x) = (x^2 + 2x + 1) / (x^2 + x) равна f'(x) = (x^2 - 1) / (x^2 + x)^2.
Это пример иллюстрирует применение правил дифференцирования к дробям с иксом в числителе и знаменателе. Следуя этим правилам, вы можете дифференцировать более сложные функции и получать точные производные.