Производная функции играет важную роль в математике и физике. Дифференцирование позволяет нам изучать изменение функции в зависимости от ее аргумента. Однако, производная некоторых функций может быть достаточно сложной и вызывать затруднения при ее вычислении.
В данной статье мы рассмотрим, как найти производную дроби, в которой переменная возведена в куб. Это может быть крайне полезным при решении задач, когда требуется найти скорость изменения функции или определить экстремумы.
Для вычисления производной дроби с x в кубе можно использовать метод дифференцирования степенной функции. Воспользуемся фактом, что производная функции x в степени n равна произведению степени и производной функции x:
f(x) = x^3
f'(x) = 3x^(3-1) = 3x^2
Таким образом, производная дроби с x в кубе будет равна 3x^2, где x - аргумент функции.
Приведем пример вычисления производной дроби с x в кубе:
f(x) = (2x^3 + 5x^2 - 3x) / (x^3 + 2x^2)
Для нахождения производной, мы можем использовать правило дифференцирования сложной функции. Пусть f(x) = u(x) / v(x), где u(x) и v(x) - функции. Тогда, производная функции f(x) будет равна:
f'(x) = (u'(x)v(x) - u(x)v'(x)) / (v(x))^2
Применим это правило для нашей функции f(x):
f'(x) = ((6x^2 + 10x - 3)(x^3 + 2x^2) - (2x^3 + 5x^2 - 3x)(3x^2 + 4x)) / (x^3 + 2x^2)^2
Выполнив вычисления, мы получим значение производной дроби с x в кубе. Это значение поможет нам лучше понять, как изменяется функция в различных точках и решать задачи, связанные с производной.
Производная дроби с x в кубе: базовые понятия и формулы
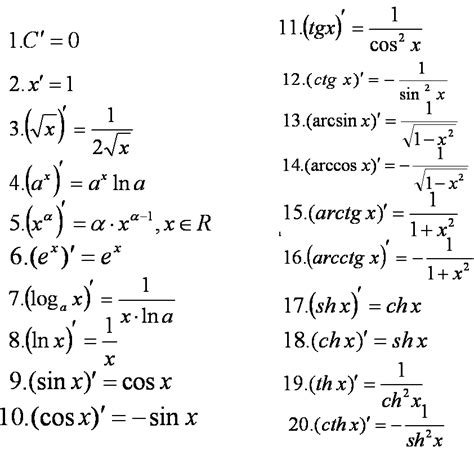
Для нахождения производной функции вида f(x) = x^3, где x - переменная, нужно использовать правило дифференцирования степенной функции. Степенная функция вида x^n имеет производную f'(x) = n * x^(n-1). В случае дроби с x в кубе, степень равна 3, поэтому производная будет равна 3 * x^(3-1), то есть 3 * x^2.
Производная дроби с x в кубе может быть записана следующим образом: f'(x) = 3 * x^2. Это означает, что в каждой точке графика функции скорость изменения будет равна произведению значения переменной x на 3 и на квадрат этого значения.
Для лучшего понимания различных случаев нахождения производной дроби с x в кубе, предлагается таблица примеров:
| Функция | Производная |
|---|---|
| f(x) = x^3 | f'(x) = 3 * x^2 |
| f(x) = 2x^3 | f'(x) = 6 * x^2 |
| f(x) = -x^3 | f'(x) = -3 * x^2 |
Таким образом, нахождение производной дроби с x в кубе сводится к применению правила дифференцирования степенной функции. В зависимости от коэффициента перед переменной x, производная может изменяться, но базовая формула остается неизменной: f'(x) = 3 * x^2. Это позволяет определить скорость изменения функции в каждой точке и провести анализ ее поведения.
Примеры решения задачи по нахождению производной дроби с x в кубе
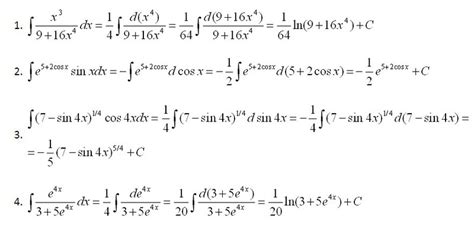
Для нахождения производной дроби с x в кубе, необходимо применить правило дифференцирования функции натурального показателя степени:
Если у нас есть функция вида f(x) = xn, где n - натуральное число, то производная этой функции будет равна f'(x) = nxn-1.
Применим это правило к нашей дроби. Рассмотрим примеры:
| Пример | Исходная функция | Производная |
|---|---|---|
| Пример 1 | f(x) = x/x3 | f'(x) = 3x2-x^3/x6 |
| Пример 2 | f(x) = x3/x^2 | f'(x) = 3x2-2x^3/x4 |
| Пример 3 | f(x) = x4/x^3 | f'(x) = 4x3-3x^4/x6 |
Это лишь некоторые примеры решения задачи по нахождению производной дроби с x в кубе. При нахождении производной дроби необходимо аккуратно применять правило дифференцирования и упрощать полученные выражения, если это возможно. Это поможет получить правильный ответ.