Производная функции – одно из важнейших понятий в математике, которое широко применяется в физике, экономике, инженерии и других областях. Производная позволяет определить скорость изменения функции в каждой точке её графика. Благодаря производной мы можем узнать, где функция имеет минимум или максимум, и изучать разные аспекты её поведения.
Найти производную функции можно с помощью различных методов, таких как правило дифференцирования степенной функции, правило дифференцирования произведения, правило дифференцирования сложной функции и другие. Каждое правило имеет свою формулу, с помощью которой можно вычислить производную функции в соответствующей точке.
Для понимания процесса нахождения производной функции, рассмотрим простой пример. Пусть дана функция f(x) = x^2. Чтобы найти производную этой функции, применим формулу для дифференцирования степенной функции. Согласно формуле, производная функции f(x) будет равна f'(x) = 2x. Таким образом, производная функции f(x) = x^2 равна f'(x) = 2x.
Что такое производная функции?

Формально, производная функции определяется как предел отношения разности значений функции в бесконечно близких точках к разности аргументов функции при стремлении этих точек друг к другу. Производная функции обозначается символом f'(x) или dy/dx.
Производная функции позволяет решать множество задач, связанных с анализом функций. Она позволяет определить экстремумы функции, то есть ее максимальные и минимальные значения, а также исследовать поведение функции в окрестности различных точек ее области определения. Кроме того, производная функции позволяет находить касательные, нормали и кривизну к графику функции в отдельных точках.
Для вычисления производной функции существуют различные методы и правила, такие как правила дифференцирования элементарных функций, правило дифференцирования композиции функций и правило дифференцирования произведения и частного функций.
Формулы для нахождения производной
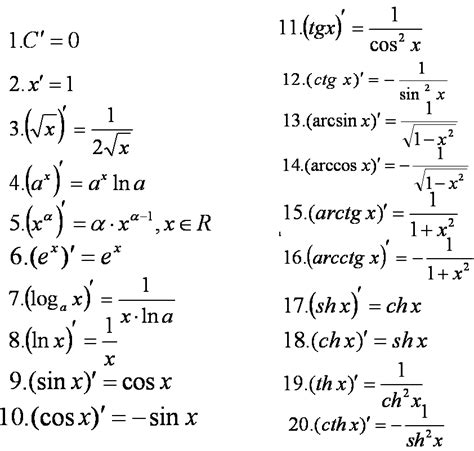
Вот некоторые из основных формул для нахождения производной:
1. Формула для производной константы:
D(c) = 0, где c – константа.
2. Формула для производной переменной:
D(x) = 1, где x – переменная.
3. Формула для производной степенной функции:
D(x^n) = nx^(n-1), где n – натуральное число.
4. Формула для производной суммы функций:
D(u + v) = D(u) + D(v), где u и v – функции.
5. Формула для производной произведения функций:
D(uv) = u * D(v) + v * D(u), где u и v – функции.
Это лишь некоторые из формул, которые используются для нахождения производной. Знание этих формул поможет вам решать задачи на дифференцирование более эффективно и точно.
Примеры нахождения производной

Найдем производные для нескольких примеров функций:
Пример 1: Найти производную функции f(x) = 3x^2 + 2x - 5.
Решение:
Используем правило производной для каждого слагаемого функции:
f'(x) = (3 * 2x^(2-1)) + (2 * 1x^(1-1)) + 0 = 6x + 2
Таким образом, производная функции f(x) равна f'(x) = 6x + 2.
Пример 2: Найти производную функции g(x) = 5sin(x).
Решение:
Используем правило производной для функции синуса:
g'(x) = 5 * cos(x)
Таким образом, производная функции g(x) равна g'(x) = 5cos(x).
Пример 3: Найти производную функции h(x) = ln(x^2).
Решение:
Используем правило производной для функции натурального логарифма:
h'(x) = 2x * 1/x^2 = 2/x
Таким образом, производная функции h(x) равна h'(x) = 2/x.
В этих примерах были использованы основные правила нахождения производной функции: правило степенной функции, правило производной для тригонометрических функций и правило производной для функции натурального логарифма. Зная эти правила, можно находить производные для различных функций.
Как решать задачи по нахождению производной?

1. Введение
Нахождение производной функции является одним из важных понятий в математике. Производная позволяет найти скорость изменения функции в каждой точке. Она имеет широкое применение в различных областях, таких как физика, экономика, инженерия и другие.
2. Определение и основные свойства производной
Производная функции в точке определяется как предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю. Производная функции описывает скорость изменения функции в данной точке.
Основные свойства производной:
- Производная константы равна нулю.
- Производная функции-монома равна произведению его показателя степени на коэффициент.
- Производная суммы функций равна сумме их производных.
- Производная произведения функций вычисляется с помощью правила произведения.
3. Как решать задачи по нахождению производной
Для решения задач по нахождению производной нужно:
- Записать данную функцию.
- Применить правила нахождения производной конкретной функции.
- Вычислить производную.
Пример решения задачи:
Задача: Найти производную функции f(x) = 3x^2 - 2x + 1.
Решение: Для нахождения производной данной функции нужно применить правило производной для каждого члена функции:
Производная функции f(x) = 3x^2 - 2x + 1:
- Производная члена 3x^2 равна 6x (по правилу производной степенной функции).
- Производная члена -2x равна -2 (по правилу производной линейной функции).
- Производная константы 1 равна 0 (по свойству производной константы).
Таким образом, производная функции f(x) = 3x^2 - 2x + 1 равна 6x - 2.
4. Заключение
Нахождение производной функции является важным инструментом для изучения функций и их свойств. Знание основных правил и методов нахождения производной позволяет решать разнообразные задачи. Практика решения задач по нахождению производной поможет улучшить понимание этого понятия и его применения в реальных задачах.
Производная сложной функции

Если функция f(x) является композицией двух функций g(x) и h(x), то ее производная f'(x) может быть найдена с помощью цепного правила, которое утверждает: производная сложной функции равна произведению производной внешней функции на производную внутренней функции.
Формула цепного правила выглядит следующим образом:
f'(x) = g'(h(x)) · h'(x)
Применение цепного правила позволяет найти производную сложной функции и расширить набор инструментов для работы с функциями, которые представляют собой композицию различных функций.
Например, пусть дана функция f(x) = (2x + 1)^3. Для нахождения ее производной применим цепное правило. В данном случае внешняя функция - возведение в куб, а внутренняя функция - линейная функция 2x + 1.
Согласно цепному правилу, производная сложной функции равна произведению производной внешней функции на производную внутренней функции. Производная внешней функции равна 3(2x + 1)^2, а производная внутренней функции равна 2.
Таким образом, производная функции f(x) = (2x + 1)^3 равна f'(x) = 3(2x + 1)^2 · 2.
Применение цепного правила позволяет находить производные сложных функций и применять их в различных задачах математического анализа и естественных наук.
Производная элементарных функций
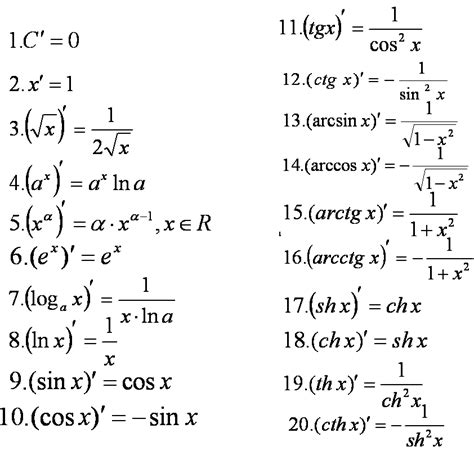
1. Степенная функция: для функции вида y = x^n, производная равна произведению показателя степени на основание, умноженное на x в степени (n-1). Например, производная функции y = x^3 будет равна 3x^2.
2. Логарифмическая функция: для функции вида y = log_a(x), производная равна производной естественного логарифма от x, деленной на логарифмическую константу. Например, производная функции y = ln(x) будет равна 1/x.
3. Экспоненциальная функция: для функции вида y = a^x, производная равна произведению естественного логарифма от основания функции на саму функцию. Например, производная функции y = e^x будет равна e^x.
4. Тригонометрическая функция: для функций типа синуса, косинуса и тангенса, производные имеют следующие значения: производная функции y = sin(x) равна cos(x), производная функции y = cos(x) равна -sin(x), а производная функции y = tan(x) равна sec^2(x), где sec(x) - это секанс от x.
Эти правила помогают нам находить производные элементарных функций и использовать их в дальнейшем построении графиков и решении уравнений.