Нахождение производной является одной из основных задач дифференциального исчисления. В данной статье мы рассмотрим процесс нахождения производной функции синуса. Синус - это тригонометрическая функция, которая описывает соотношение между сторонами и углами прямоугольного треугольника. Производная синуса позволяет найти скорость изменения этой функции в каждой ее точке.
Для начала, мы будем использовать основное правило дифференцирования, которое гласит: производная синуса равна косинусу данного угла. Косинус, также являющийся тригонометрической функцией, измеряет соотношение сторон прямоугольного треугольника. Подставив это правило в формулу дифференцирования, мы получаем, что производная синуса равна косинусу угла:
f'(x) = cos(x)
Теперь, имея формулу для производной синуса, мы можем приступить к нахождению производных сложных функций, где функция синуса является составной частью. Для этого мы используем правило дифференцирования сложных функций, которое позволяет найти производную сложной функции через производные ее составных частей.
Зачем нужно знать производную синуса
Одной из основных причин знать производную синуса является возможность определить максимумы и минимумы этой функции. Производная показывает, где график функции синуса меняет свое направление, что позволяет найти точки экстремума. Например, это может быть полезно при решении задач, связанных с оптимизацией, когда требуется найти максимальное или минимальное значение функции синуса в определенном интервале.
Кроме того, знание производной синуса позволяет определить скорость изменения этой функции в данной точке. По производной можно судить о том, насколько быстро меняется значение синуса вблизи определенной точки. Это может быть полезно, например, при анализе движения тела синусоидальной формы или при моделировании осцилляций в физических системах.
Также, знание производной синуса может быть полезным при решении определенных дифференциальных уравнений, в которых функция синуса является частью решения. Зная производную, мы можем точно выразить эту функцию и найти ее значение в нужной точке.
В целом, умение находить производную функции синуса расширяет наши возможности в решении различных задач и дает нам лучшее понимание самой функции синуса и ее свойств.
Как определить производную функции синуса

Правило дифференцирования для функции синуса устанавливает, что производная функции sin(x) равна cos(x):
d/dx(sin(x)) = cos(x)
То есть, чтобы найти производную sin(x) по x, достаточно заменить sin(x) на cos(x).
Важно помнить, что дифференцирование можно проводить только по переменной, а все остальные элементы в функции остаются без изменений.
Например, если мы хотим найти производную функции 2sin(x), то сначала мы заменяем sin(x) на cos(x):
d/dx(2sin(x)) = 2cos(x)
Итак, чтобы найти производную функции синуса, мы просто заменяем sin(x) на cos(x).
Также, стоит помнить, что функция cos(x) является производной функции sin(x), поэтому производная функции cos(x) будет равна -sin(x):
d/dx(cos(x)) = -sin(x)
Это правило также можно использовать для нахождения производной функций, содержащих синус и косинус.
Теперь, когда вы знаете основные правила нахождения производной функции синуса, вы можете использовать их для решения задач по дифференцированию и анализу функций.
Шаг 1: Запись функции синуса
Математическая запись функции синуса выглядит следующим образом:
| sin(x) |
Где "x" - это аргумент функции, который может быть числом или переменной.
Производная функции показывает, как быстро функция меняется в каждой точке. Для нахождения производной функции синуса, мы будем использовать основные правила дифференцирования исходных функций.
Шаг 2: Использование основных правил дифференцирования
После того, как мы установили функцию, которую необходимо дифференцировать, переходим к использованию основных правил дифференцирования. Для функции синуса мы можем применить следующее правило:
Правило: дифференциал синуса функции f(x) равен произведению дифференциала самой функции f(x) на косинус f'(x).
Другими словами, чтобы найти производную функции синуса, мы должны дифференцировать саму функцию и умножить результат на косинус этой функции.
Применяя это правило к функции синуса, мы получаем следующее выражение:
d(sin(x))/dx = cos(x)
Таким образом, производная функции синуса равна косинусу этой функции.
Используя это правило, мы можем дифференцировать функцию синуса и получить производную этой функции.
Шаг 3: Пошаговый расчет производной

Для расчета производной функции синуса, нам потребуется применить несколько правил дифференцирования. Давайте посмотрим, как это сделать.
1. Начнем с исходной функции: f(x) = sin(x)
2. Применим правило дифференцирования функции синуса: d(sin(x))/dx = cos(x)
3. Таким образом, производная функции синуса равна функции косинуса: f'(x) = cos(x)
Теперь у нас есть конечный результат - производная функции синуса, которая равна функции косинуса. Это правило может быть использовано для нахождения производной функции синуса в любой точке.
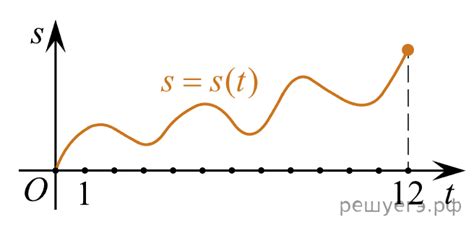
Обратите внимание, что производная функции синуса является периодической функцией, как и сама функция синуса. Это также может быть представлено графически, повторяющимся паттерном, где значение производной меняется от положительного до отрицательного и обратно при переходе через каждую полную окружность.
Шаг 4: Проверка найденной производной
После того, как мы вычислили производную функции синуса на предыдущих шагах, необходимо провести проверку правильности полученного результата. Это важно, потому что ошибки при вычислении производной могут быть допущены.
Для проверки найденной производной можно использовать несколько методов:
1. Графический метод: Построить график функции синуса и ее производной на одном графике. Если полученные графики совпадают, то это свидетельствует о правильности найденной производной.
2. Подстановка значения: Подставить значение переменной в исходную функцию синуса и в ее производную, полученную на предыдущих шагах. Если значения совпадают, то производная была найдена правильно.
3. Геометрический метод: Использовать геометрические свойства функции синуса и ее производной для проверки. Например, производная синуса равна косинусу, поэтому можно построить прямоугольный треугольник, где один из углов равен значению переменной, а сторона, противолежащая этому углу, равна значению производной. Если получаемый треугольник соответствует геометрическим свойствам синуса и его производной, то производная найдена верно.
Проведение проверки поможет убедиться в правильности найденной производной и избежать возможных ошибок при дальнейших вычислениях и анализе функции.
Шаг 5: Интерпретация результата

После всех предыдущих шагов, мы нашли производную функции синуса, которая равна значению косинуса функции в данной точке. Итак, если нам дана функция синуса и нам нужно найти производную этой функции, мы можем использовать косинус, чтобы получить итоговый результат.
Интерпретация этого результата заключается в понимании, что производная функции синуса дает нам скорость изменения значения функции в каждой точке. Если производная положительна, значит функция синуса растет, а если она отрицательна, то функция убывает. Кроме того, значение производной позволяет нам определить, насколько быстро функция синуса меняет свое значение в данной точке.
Итак, на этом шаге мы можем сказать, что производная функции синуса показывает нам скорость и направление изменения значения функции в каждой точке. Это важное понятие, которое имеет широкий спектр применений в математическом анализе и физике.
Примеры нахождения производной функции синуса

Для нахождения производной функции синуса, которая обозначается как d(sin(x))/dx или (sin(x))', необходимо применить правило дифференцирования синуса.
Правило дифференцирования синуса гласит:
d(sin(x))/dx = cos(x)
Вот несколько примеров применения этого правила:
- Для функции f(x) = sin(x):
- Производная функции f(x) равна f'(x) = cos(x)
- Применяем правило дифференцирования синуса и правило умножения:
- Производная функции g(x) равна g'(x) = 2cos(3x) * 3 = 6cos(3x)
- Применяем правило степенной функции и правило дифференцирования синуса:
- Производная функции h(x) равна h'(x) = 2sin(x) * cos(x)
Таким образом, нахождение производной функции синуса сводится к применению соответствующих правил дифференцирования.