Радиус круга - один из основных параметров, определяющих его геометрические характеристики. Его значение является ключевым при расчете площади, длины окружности и других параметров круга. Однако, иногда возникает необходимость найти радиус круга по уже известным показателям, например, по его площади или углу. В этой статье мы подробно рассмотрим формулы и примеры, которые позволят вам находить радиус круга при заданных условиях.
Если известна площадь круга, то радиус можно найти с помощью формулы:
r = √(S/π),
где r - радиус круга, S - площадь круга, π - математическая константа "пи", примерно равная 3.14.
Если известен угол круга в радианах, то радиус можно вычислить по формуле:
r = l/θ,
где r - радиус круга, l - длина окружности круга, θ - угол (в радианах).
Давайте рассмотрим примеры, чтобы лучше понять, как применять эти формулы на практике.
Как найти радиус круга?

Существует несколько способов определить радиус круга. Один из них - использование формулы, связывающей радиус и площадь круга. Для этого необходимо знать площадь круга и применить следующую формулу:
Радиус = √(Площадь / Пи)
В этой формуле "Площадь" - это площадь круга, а "Пи" - математическая константа, приближенное значение которой равно 3,14159. Итак, чтобы узнать радиус круга, нужно разделить его площадь на Пи и затем извлечь квадратный корень из полученного значения. Результат будет равен радиусу круга.
Например, предположим, что площадь круга равна 25 квадратным сантиметрам. Применяя формулу, получаем:
Радиус = √(25 / 3,14159) ≈ √7,9577 ≈ 2,82 (см)
Таким образом, радиус круга равен примерно 2,82 сантиметра.
Определение радиуса круга по площади и углу также возможно, но требует более сложных расчетов и специфических формул. В таких случаях рекомендуется обратиться к специалисту или использовать специализированные программы или онлайн-калькуляторы.
Формула для нахождения радиуса круга по площади
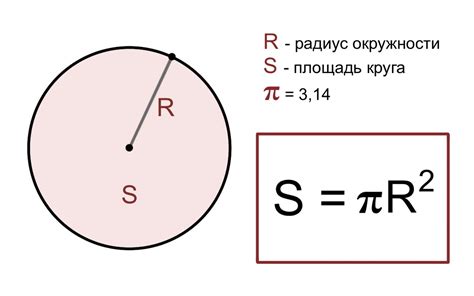
Для нахождения радиуса круга по известной площади можно использовать следующую формулу:
| S = π * r^2 |
где:
S - площадь круга,
π (пи) - математическая константа, примерное значение которой равно 3.14159,
r - радиус круга.
Для нахождения радиуса круга по данной формуле необходимо выполнить следующие шаги:
Значение площади круга известно, подставьте его в формулу.
Значение π (пи) известно, возьмите примерное значение 3.14159.
Решите уравнение относительно r, выразив радиус круга.
Например, пусть площадь круга равна 25 квадратным сантиметрам. Подставляя значение площади в формулу, получаем:
| 25 = 3.14159 * r^2 |
Решая уравнение относительно r, мы можем выразить радиус круга:
| r^2 = 25 / 3.14159 |
| r ≈ √(7.9577) |
| r ≈ 2.82 |
Таким образом, для круга с площадью 25 квадратных сантиметров радиус будет примерно равен 2.82 сантиметра.
Формула для нахождения радиуса круга по углу
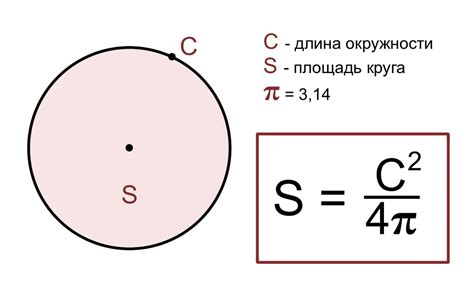
Для нахождения радиуса круга по углу и площади можно использовать следующую формулу:
r = sqrt(S / (π * α))
где:
- r - радиус круга,
- S - площадь круга,
- α - угол (в радианах),
- π (пи) - математическая константа, приближенное значение которой равно 3.14159.
Пример использования формулы:
Дано: площадь круга равна 25 квадратных сантиметров, угол составляет 45 градусов.
Сначала нужно перевести угол из градусов в радианы. Для этого воспользуемся следующей формулой:
αрад = (αград * π) / 180
Подставив значения в формулу, получим:
αрад = (45 * 3.14159) / 180 = 0.7854 радиан
Теперь можем использовать формулу для нахождения радиуса круга:
r = sqrt(25 / (3.14159 * 0.7854))
Вычислим значение:
r ≈ sqrt(31.831) ≈ 5.64 сантиметра
Таким образом, радиус круга составляет примерно 5.64 сантиметра.
Примеры расчета радиуса круга

Рассмотрим несколько примеров, чтобы лучше понять, как найти радиус круга по его площади и углу.
Пример 1:
Площадь круга равна 50 квадратных сантиметров. Найдите радиус круга.
Чтобы найти радиус круга, воспользуемся формулой: Радиус = √(Площадь / π)
В данном случае, площадь равна 50 см², поэтому:
Радиус = √(50 / π) ≈ √(15.92) ≈ 3.99 см
Пример 2:
Круг описывается углом в 60 градусов. Найдите радиус круга.
Известно, что угол вписанной дуги составляет половину центрального угла, поэтому центральный угол равен 120 градусам.
Для нахождения радиуса круга в данном случае можно воспользоваться тригонометрической формулой Радиус = Длина дуги / (угол в градусах * π / 180).
Если известно, что длина дуги равна 10 сантиметров, то:
Радиус = 10 / (120 * π / 180) ≈ 10 / 2.094 ≈ 4.77 см
Пример 3:
Площадь круга равна 100 квадратных метров. Найдите радиус круга.
Воспользуемся формулой для нахождения радиуса круга по его площади: Радиус = √(Площадь / π).
В данном случае, площадь равна 100 м²:
Радиус = √(100 / π) ≈ √(31.83) ≈ 5.64 м