Окружность - это одна из основных геометрических фигур, которая имеет бесконечное количество точек на определенном расстоянии от центра. При изучении окружностей нередко встает вопрос о нахождении радиуса, основного параметра, который определяет размер окружности.
Существует несколько методов для определения радиуса окружности, однако, одним из самых простых является расчет по площади и центральному углу. Вам может понадобиться найти радиус, когда площадь окружности или центральный угол известны. В таких случаях следует использовать соответствующую формулу.
Данная формула основывается на теории треугольников, а именно теореме синусов. Если известна площадь окружности (S) и центральный угол (α), то радиус (R) можно вычислить по формуле: R = √(S / (π * sin(α)))
Таким образом, зная площадь и центральный угол, достаточно подставить значения в формулу и выполнить несложные арифметические вычисления, чтобы получить необходимый результат. Этот метод позволяет быстро и удобно вычислить радиус окружности и использовать его для решения задач в геометрии.
Понятие радиуса окружности
Первое свойство – радиус окружности одинаков для всех ее точек. Это означает, что любой отрезок, соединяющий центр окружности с любой ее точкой, будет иметь одинаковую длину.
Второе свойство связано с площадью окружности. Площадь окружности можно вычислить по формуле: S = π * r^2, где S – площадь, π – число Пи (приближенное значение 3.14) и r – радиус окружности.
Третье свойство радиуса – его влияние на центральный угол. Если провести любой радиус окружности, то он будет являться стороной центрального угла, образованного этим радиусом и двумя лежащими на окружности точками. Значение этого угла зависит от длины радиуса и положения точек на окружности.
Радиус окружности играет важную роль в геометрии и нахождении других параметров окружностей. Зная его значение, можно вычислить длину окружности, площадь и другие свойства фигуры. Поэтому понимание понятия радиуса окружности является основой для изучения геометрии и решения геометрических задач.
Расчет радиуса с помощью площади
Формула для расчета радиуса окружности с известной площадью имеет вид:
r = √(S/π)
где r - радиус окружности, S - площадь окружности, π - математическая константа, примерно равная 3.14159.
Для примера, предположим, что площадь окружности равна 25 квадратных метров. Чтобы найти радиус, мы применим формулу:
r = √(25/π) ≈ √8 ≈ 2.828
Поэтому радиус окружности с площадью 25 квадратных метров примерно равен 2.828 метра.
Используя данную формулу, вы можете легко и быстро вычислить радиус окружности, если площадь известна.
Формула для расчета радиуса по площади окружности
Формула для расчета радиуса по площади окружности выглядит следующим образом:
- Определите площадь окружности.
- Используйте следующую формулу: Радиус = √(Площадь / Пи)
Где:
- Радиус - значение, которое мы ищем.
- Площадь - известное значение площади окружности.
- Пи - математическая константа, приближенно равная 3,14159.
Пример использования формулы:
- Площадь окружности равна 25 единицам квадратных.
- Используем формулу: Радиус = √(25 / 3,14159).
- Вычисляем значение: Радиус = √(7,9577).
- Получаем ответ: Радиус ≈ 2,8197.
Таким образом, для вычисления радиуса окружности по известной площади, просто используйте эту формулу и подставьте известные значения. Не забывайте округлять результат до необходимой точности.
Расчет радиуса с помощью центрального угла

Угол, накрывающий дугу окружности, называется центральным углом. Радиус окружности можно вычислить, если известна площадь сектора и центральный угол.
Для расчета радиуса окружности по известной площади и центральному углу сначала необходимо вычислить длину дуги окружности по формуле:
S = r * α
где S - площадь сектора, r - радиус окружности, α - центральный угол в радианах.
Затем необходимо найти длину окружности по формуле:
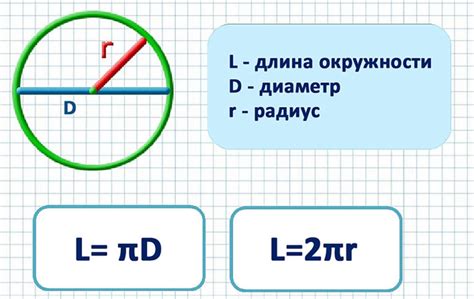
C = 2πr
где С - длина окружности, r - радиус окружности, π - математическая константа, приближенное значение которой равно 3,14.
Длина дуги окружности равна длине окружности, поэтому выражая радиус через известные величины, получаем:
r = S / α
Таким образом, для расчета радиуса окружности с известной площадью сектора и центральным углом необходимо разделить площадь на центральный угол в радианах.
Формула для расчета радиуса по центральному углу и длине дуги
Если вам известен центральный угол и длина дуги, мы можем использовать следующую формулу для расчета радиуса окружности:
Радиус = (длина дуги * 180) / (центральный угол * π)
В этой формуле длина дуги измеряется в единицах длины (например, метрах или сантиметрах), а центральный угол указывается в градусах.
Давайте рассмотрим пример. Пусть центральный угол окружности равен 60 градусов, а длина дуги составляет 10 метров. Как найти радиус?
Применяя нашу формулу, мы получаем:
| Длина дуги (м) | Центральный угол (градусы) | Радиус (м) |
|---|---|---|
| 10 | 60 | (10 * 180) / (60 * 3.1416) ≈ 0.953 |
Таким образом, радиус окружности составит примерно 0.953 метра.
Теперь у вас есть формула для расчета радиуса по центральному углу и длине дуги. Вы можете использовать ее для решения различных геометрических задач, связанных с окружностями.
Примеры решения задач:

Рассмотрим несколько примеров расчета радиуса окружности с известной площадью и центральным углом:
| Пример | Площадь (S) | Центральный угол (α) | Радиус (r) |
|---|---|---|---|
| Пример 1 | 9 кв. ед. | 60° | 3 ед. |
| Пример 2 | 16.5 кв. см | 45° | 2.5 см |
| Пример 3 | 25 кв. м | 90° | 5 м |
Для вычисления радиуса окружности в этих примерах можно воспользоваться формулой:
r = √(S / (π * α / 180))
Где:
r - радиус окружности;
S - площадь окружности;
α - центральный угол в градусах;
π - число Пи, примерное значение 3.14.
Подставляя значения из примеров в формулу, получаем следующие расчеты радиуса:
Пример 1:
r = √(9 / (π * 60 / 180)) ≈ √(9 / 0.523) ≈ √(9 / 0.523) ≈ √(17.214) ≈ 3 ед.
Пример 2:
r = √(16.5 / (π * 45 / 180)) ≈ √(16.5 / 0.785) ≈ √(20.991) ≈ 2.5 см
Пример 3:
r = √(25 / (π * 90 / 180)) ≈ √(25 / 1.57) ≈ √(15.924) ≈ 5 м
Таким образом, мы можем использовать данную формулу для нахождения радиуса окружности при известной площади и центральном угле.
Пример 1: Нахождение радиуса окружности с заданной площадью
Представим себе, что у нас есть задача найти радиус окружности с известной площадью. Для решения этой задачи мы можем воспользоваться простой формулой, которая связывает площадь окружности и ее радиус.
Дано:
- Площадь окружности: S
Решение:
Формула для нахождения площади окружности выглядит следующим образом:
S = pi * r^2
где S - площадь окружности, pi - число Пи (приблизительно равно 3.14159), r - радиус окружности.
Чтобы найти радиус окружности, нужно переписать формулу в следующем виде:
r = sqrt(S / pi)
где sqrt() - функция квадратного корня.
Теперь подставим известное значение площади окружности в формулу и вычислим радиус:
r = sqrt(S / pi)
Таким образом, мы можем найти радиус окружности, если известна ее площадь.