Вписанный треугольник в окружность - это треугольник, все вершины которого лежат на окружности. Это геометрическая фигура, которая вызывает интерес и изучается в математике. Одним из важных параметров вписанного треугольника является радиус окружности, которой он описан. В этой статье мы рассмотрим, как найти радиус окружности с вписанным треугольником и представим формулу, с помощью которой это можно сделать.
Для начала вспомним некоторые особенности вписанного треугольника. Вписанный треугольник имеет три биссектрисы, которые пересекаются в одной точке - центре окружности, на которой он описан. Это значит, что отрезки, соединяющие вершины треугольника с центром окружности, являются радиусами окружности.
Величина радиуса окружности с вписанным треугольником играет важную роль при решении различных задач и задач геометрического анализа. Для нахождения радиуса существуют несколько подходов. Один из них основан на использовании формулы, в которой участвуют длины сторон треугольника.
Пусть a, b и c - длины сторон треугольника, а R - радиус окружности с вписанным треугольником. Тогда формула для нахождения радиуса R имеет вид:
Где p - полупериметр треугольника и вычисляется по формуле:
Таким образом, нахождение радиуса окружности с вписанным треугольником сводится к нахождению длин сторон треугольника и использованию соответствующих формул. Это позволяет удобно решать различные задачи, связанные с треугольником и его окружностью.
Что такое радиус окружности с вписанным треугольником?

Радиус окружности с вписанным треугольником играет важную роль при решении различных геометрических задач. Он связан с основными характеристиками треугольника и влияет на его форму и размеры. Зная значение радиуса окружности с вписанным треугольником, можно вычислить длины сторон, углы и другие параметры треугольника.
Для вычисления радиуса окружности с вписанным треугольником существует специальная формула, которая зависит от сторон и углов треугольника. Она выражается следующим образом:
| Радиус окружности с вписанным треугольником: | r = a / (2 * sin(A)) |
Где:
- r - радиус окружности с вписанным треугольником
- a - длина одной из сторон треугольника
- A - угол между стороной a и смежной стороной
Используя данную формулу, можно вычислить радиус окружности с вписанным треугольником и далее применять его для решения геометрических задач.
Объяснение и геометрическое определение

Геометрическое определение радиуса окружности с вписанным треугольником заключается в следующем: если провести радиус из центра окружности к одной из вершин треугольника, он будет перпендикулярен соответствующей стороне треугольника. Таким образом, все три радиуса, проведенные из центра окружности к вершинам треугольника, являются перпендикулярными к соответствующим сторонам треугольника.
Радиус окружности с вписанным треугольником может быть найден с использованием формулы, связывающей радиус, площадь треугольника и его полупериметр. Формула для нахождения радиуса окружности вписанного треугольника выглядит следующим образом:
Радиус = Площадь треугольника / Полупериметр треугольника
Здесь площадь треугольника вычисляется с использованием формулы Герона, которая зависит от длин его сторон, а полупериметр треугольника представляет собой половину суммы длин его сторон.
Нахождение радиуса окружности с вписанным треугольником может быть полезно при решении различных задач геометрии, например, при определении точки пересечения биссектрис треугольника или нахождении высоты треугольника, проведенной из вершины к основанию.
Как найти радиус окружности с вписанным треугольником?
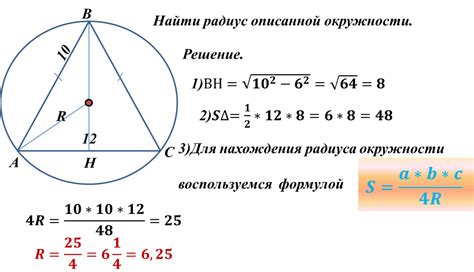
Для вычисления радиуса окружности с вписанным треугольником можно использовать формулу:
Здесь:
- r - радиус вписанной окружности;
- A, B, C - углы треугольника (измеряемые в радианах).
Используя данную формулу, вы можете вычислить радиус окружности с вписанным треугольником при известных значениях углов треугольника.
Например, если вам известны значения углов треугольника (A = 60°, B = 45°, C = 75°), вы можете вычислить радиус окружности с помощью формулы и получить точное значение для дальнейших расчетов или анализа.
Это была формула и объяснение, как найти радиус окружности с вписанным треугольником.
Подробный алгоритм и формула
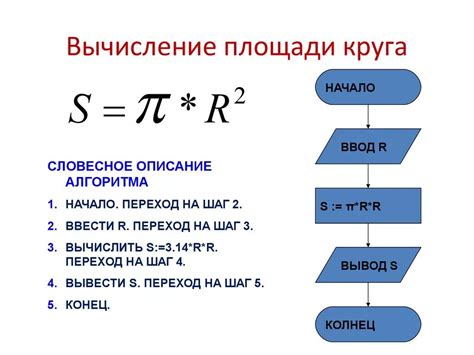
Для нахождения радиуса окружности, вписанной в треугольник, нужно выполнить следующие шаги:
- Найти длины всех сторон треугольника.
- Вычислить полупериметр треугольника по формуле: p = (a+b+c)/2, где a, b и c - длины сторон треугольника.
- Вычислить площадь треугольника по формуле Герона: S = sqrt(p*(p-a)*(p-b)*(p-c)).
- Найти радиус окружности, вписанной в треугольник, по формуле: r = S / p.
Теперь у нас есть подробный алгоритм для нахождения радиуса окружности, вписанной в треугольник, и соответствующая ему формула.
| Шаг | Действие | Формула |
|---|---|---|
| 1 | Найти длины всех сторон треугольника | - |
| 2 | Вычислить полупериметр треугольника | p = (a+b+c)/2 |
| 3 | Вычислить площадь треугольника | S = sqrt(p*(p-a)*(p-b)*(p-c)) |
| 4 | Найти радиус окружности | r = S / p |
Этот алгоритм и формула позволяют точно и быстро найти радиус окружности, вписанной в треугольник.
Примеры решения задачи на нахождение радиуса окружности с вписанным треугольником
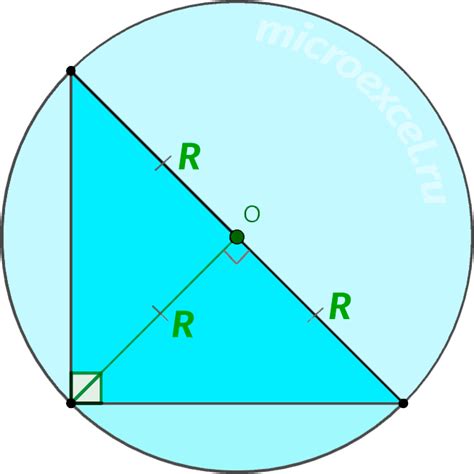
Для решения задачи на нахождение радиуса окружности с вписанным треугольником можно использовать следующую формулу:
Радиус окружности с вписанным треугольником равен половине отношения длины одной из сторон треугольника к полупериметру треугольника.
Формула выглядит следующим образом:
Радиус = a / (2 * sin(π/n)),
- где a - длина одной из сторон треугольника,
- n - количество сторон треугольника (обычно равно 3 для вписанного треугольника).
Если известны длина стороны треугольника и количество его сторон, можно легко найти радиус окружности с помощью данной формулы.
Пример решения задачи:
- Известно, что у вписанного треугольника длина стороны равна 6 единицам.
- Также известно, что треугольник имеет 3 стороны.
- Для нахождения радиуса воспользуемся формулой: Радиус = a / (2 * sin(π/n)).
- Подставляем известные значения: Радиус = 6 / (2 * sin(π/3)).
- Вычисляем sin(π/3) = √3/2.
- Подставляем в формулу: Радиус = 6 / (2 * √3/2).
- Сокращаем: Радиус = 3 / √3 = √3.
Таким образом, радиус окружности с вписанным треугольником равен √3 единицам.
Важно помнить, что данный метод применим только для вписанных треугольников, у которых все стороны касаются окружности.
