Как найти радиус описанной окружности прямоугольного треугольника в трех шагах

Прямоугольные треугольники являются основой геометрии и встречаются во множестве задач и проблем. Одной из таких задач является определение радиуса описанной окружности прямоугольного треугольника. Данная задача представляет определенный интерес, так как радиус описанной окружности имеет прямое отношение к структурным и геометрическим свойствам треугольника. Знание радиуса описанной окружности может быть полезным при решении различных задач, включая вычисление площади треугольника, определение его периметра и т.д.

Описанная окружность прямоугольного треугольника представляет собой окружность, которая проходит через все три вершины треугольника. Если известны длины сторон треугольника, то радиус описанной окружности можно найти с помощью специальной формулы. Это позволяет упростить задачу и получить точный результат.

Для нахождения радиуса описанной окружности прямоугольного треугольника можно воспользоваться теоремой описанных окружностей. Согласно этой теореме, произведение длин двух катетов треугольника равно произведению радиуса окружности на длину гипотенузы. То есть, если a и b - длины катетов, а c - длина гипотенузы, то a * b = r * c, где r - радиус описанной окружности.

Исходя из этой формулы, радиус описанной окружности прямоугольного треугольника можно выразить следующим образом: r = (a * b) / c, где a и b - длины катетов, а c - длина гипотенузы.

Описание задачи

Для решения этой задачи мы можем использовать свойства прямоугольных треугольников:

• Сторона прямоугольного треугольника, лежащая напротив прямого угла, является гипотенузой.
• Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы (известна как теорема Пифагора).
• Основное свойство описанной окружности прямоугольного треугольника состоит в том, что радиус описанной окружности равен половине длины гипотенузы.

Таким образом, чтобы найти радиус описанной окружности прямоугольного треугольника, нужно:

1. Найти длины катетов и гипотенузы прямоугольного треугольника.
2. Найти половину длины гипотенузы.

Таким образом, радиус описанной окружности будет равен половине длины гипотенузы прямоугольного треугольника.

Найдите радиус описанной окружности

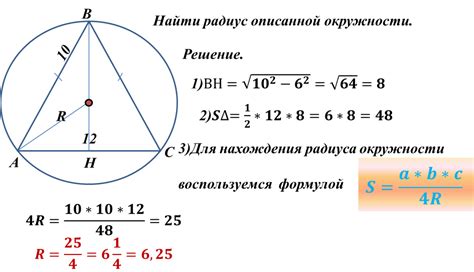
Радиус описанной окружности прямоугольного треугольника может быть найден с помощью известных формул, которые связывают его с известными сторонами этого треугольника.

Позвольте нам вспомнить несколько важных понятий:

Теперь мы можем перейти к самому важному шагу - вычислению радиуса описанной окружности.

Для этого можно воспользоваться формулой:

где R - радиус описанной окружности, c - гипотенуза прямоугольного треугольника.

Теперь, когда у вас есть формула, вы можете легко находить радиус описанной окружности для различных прямоугольных треугольников. Примените эту формулу и узнайте радиус, используя известные вам значения сторон.

Это все! Теперь вы знаете, как найти радиус описанной окружности прямоугольного треугольника. Успехов в математике!

Метод 1: Формула вписанной окружности

Для нахождения радиуса описанной окружности прямоугольного треугольника можно использовать формулу вписанной окружности. Формула основана на свойствах прямоугольного треугольника и диаграммы, которая может быть построена на основе треугольника.

Формула вписанной окружности гласит:

r = (a + b - c) / 2

где:

• r - радиус описанной окружности
• a и b - катеты прямоугольного треугольника
• c - гипотенуза треугольника

Для использования данной формулы необходимо знать значения катетов и гипотенузы треугольника. Учитывайте, что формула работает только для прямоугольных треугольников. Если треугольник не является прямоугольным, данный метод не применим.

Пример использования формулы:

Пусть у нас есть прямоугольный треугольник с катетами a = 3 и b = 4 и гипотенузой c = 5. Применяя формулу вписанной окружности, мы можем найти радиус описанной окружности:

r = (3 + 4 - 5) / 2 = 1

Таким образом, радиус описанной окружности прямоугольного треугольника равен 1.

Метод 1 является одним из подходов для нахождения радиуса описанной окружности прямоугольного треугольника. Существуют и другие методы, которые могут быть использованы для решения данной задачи.

Следуйте формуле, чтобы найти радиус описанной окружности

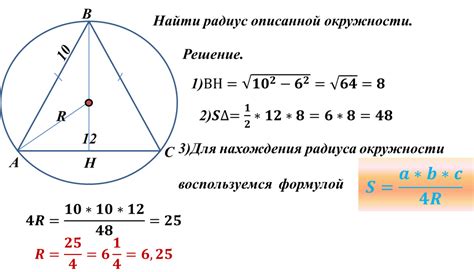
Для того чтобы найти радиус описанной окружности прямоугольного треугольника, можно воспользоваться следующей формулой:

R = a / 2,

где R - радиус описанной окружности, а a - длина гипотенузы треугольника.

Описанная окружность прямоугольного треугольника проходит через все его вершины и имеет центр, который является пересечением середин дуг трех его сторон. Радиус этой окружности равен половине длины гипотенузы треугольника.

Узнав радиус описанной окружности, вы сможете легко решать задачи, связанные с прямоугольными треугольниками и находить различные параметры этой фигуры.

Зная радиус описанной окружности прямоугольного треугольника, вы сможете найти такие величины, как длина сторон треугольника, площадь и его высоты.

Метод 2: Теорема Пифагора и радиус описанной окружности

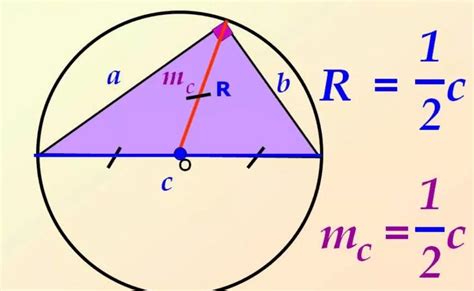
Суть этого метода заключается в следующем:

1. Найдите значение гипотенузы треугольника, используя теорему Пифагора. По этой теореме сумма квадратов катетов равна квадрату гипотенузы.

2. Разделите полученное значение гипотенузы на 2.

3. Найдите площадь треугольника, используя формулу S = (a * b) / 2, где a и b - длины катетов треугольника.

4. Вычислите радиус описанной окружности по формуле R = (a * b * c) / (4 * S), где a, b и c - стороны треугольника, а S - площадь.

Пример:

Пусть у нас есть прямоугольный треугольник со сторонами a = 3 и b = 4.

Сначала найдем гипотенузу по теореме Пифагора:

a^2 + b^2 = c^2

3^2 + 4^2 = 9 + 16 = 25

c = sqrt(25) = 5

Теперь найдем площадь треугольника:

S = (a * b) / 2 = (3 * 4) / 2 = 12 / 2 = 6

И, наконец, найдем радиус описанной окружности:

R = (a * b * c) / (4 * S) = (3 * 4 * 5) / (4 * 6) = 60 / 24 = 2.5

Таким образом, радиус описанной окружности прямоугольного треугольника со сторонами 3 и 4 равен 2.5.

Используйте теорему Пифагора для нахождения радиуса описанной окружности

Для нахождения радиуса описанной окружности прямоугольного треугольника, мы можем использовать теорему Пифагора. Предположим, что дан прямоугольный треугольник с катетами a и b и гипотенузой c.

Согласно теореме Пифагора, у нас действует следующее равенство:

a² + b² = c²

Теперь мы можем использовать это равенство для нахождения значения гипотенузы c, зная значения катетов a и b.

Зная значения гипотенузы и радиуса описанной окружности, мы можем использовать формулу для нахождения площади окружности, а именно:

S = πr²

где r - радиус описанной окружности.

Таким образом, используя теорему Пифагора, мы можем вывести формулу для нахождения радиуса описанной окружности прямоугольного треугольника и далее использовать его для вычисления площади окружности.