Радиус сектора окружности – это один из важнейших параметров, определяющих форму и размеры данной геометрической фигуры. Знание этого значения позволяет решать множество задач, связанных с окружностями и кругами. Умение находить радиус сектора является неотъемлемой частью математической грамотности и может быть полезно в решении задач из различных областей знаний, таких как геометрия, физика, инженерия и других.
Радиус сектора окружности может быть найден по известным данным, связанным с данным сектором. Одним из основных способов нахождения радиуса сектора является использование известных углов или длин дуги и хорды, соединяющей концы сектора. Кроме того, имеются также и другие методы расчета радиуса сектора, которые могут быть полезны в различных ситуациях.
Например, если известна длина дуги сектора и соответствующий ей центральный угол, радиус можно вычислить по формуле R = L / α, где R – радиус сектора, L – длина дуги, α – центральный угол в радианах. Этот метод особенно полезен при работе с системами координат или в задачах, связанных с исследованием траекторий движения.
В данной статье мы рассмотрим различные методы нахождения радиуса сектора окружности и познакомимся с примерами и оперативными формулами, которые помогут вам легко и точно решать подобные задачи. Узнаете, как измерить центральный угол, длину дуги, хорду и другие параметры, необходимые для расчета радиуса сектора окружности. Вы сможете применить полученные знания в школе, на работе или в повседневной жизни.
Методы нахождения радиуса сектора окружности
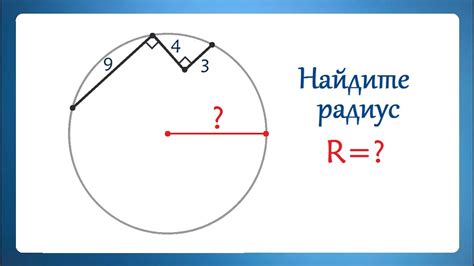
Существует несколько методов для определения радиуса сектора окружности:
- Использование длины дуги и центрального угла: Для нахождения радиуса сектора, если известны длина дуги окружности и центральный угол, можно воспользоваться формулой r = L / θ, где r - радиус сектора, L - длина дуги, а θ - центральный угол в радианах.
- Использование площади сектора и центрального угла: Если известны площадь сектора и центральный угол, радиус сектора можно найти по формуле r = √(A / πθ), где r - радиус сектора, A - площадь сектора, а θ - центральный угол в радианах.
- Использование площади треугольника и длин его сторон: Если известны площадь сектора и длины двух сторон треугольника, которые образуют радиус сектора с центральным углом, можно воспользоваться формулой r = (a * b * c) / (4A), где r - радиус сектора, a, b и c - длины сторон треугольника, а A - площадь треугольника.
Выбор метода зависит от имеющихся данных и условий задачи. При использовании этих методов необходимо учитывать правильное преобразование единиц измерения и вычисления углов в радианы, если они даны в градусах.
Геометрический способ и его особенности
Особенностью геометрического способа является его простота и доступность для понимания и применения. Для его использования необходимо знать значения длины дуги окружности и центрального угла сектора.
Формула, позволяющая найти радиус сектора окружности, выглядит следующим образом:
r = \(\dfrac{l}{\alpha}\),
где r - радиус сектора, l - длина дуги окружности, \(\alpha\) - центральный угол сектора.
Важно отметить, что в данной формуле все величины измеряются в одной системе измерения, например, в сантиметрах или метрах.
Применение геометрического способа позволяет точно определить радиус сектора окружности и использовать его в различных задачах, связанных с геометрией, строительством, механикой и другими областями науки и техники.
Тригонометрический подход и формула синусов
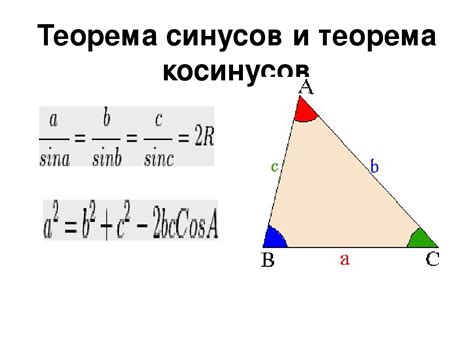
Для вычисления радиуса сектора окружности можно использовать тригонометрический подход. С помощью формулы синусов можно определить значение радиуса, зная длину дуги и угол сектора. Формула синусов позволяет найти отношение соответствующей стороны треугольника к длине противолежащего ей угла.
Пусть длина дуги окружности равна L, а угол сектора - α. Чтобы найти радиус сектора, нужно воспользоваться формулой:
R = L / (2 * sin (α / 2))
Где R - радиус сектора, L - длина дуги, α - угол сектора.
Этот подход основан на свойствах треугольника, в котором радиус окружности является гипотенузой, а длина дуги - противолежащей стороной угла сектора.
Например, если длина дуги равна 10 см, а угол сектора составляет 60 градусов, то радиус сектора можно вычислить следующим образом:
R = 10 / (2 * sin (60 / 2)) = 10 / (2 * sin (30)) = 10 / (2 * 0.5) = 10 / 1 = 10 см
Таким образом, радиус сектора окружности равен 10 см.
Использование угла и длины дуги для нахождения радиуса
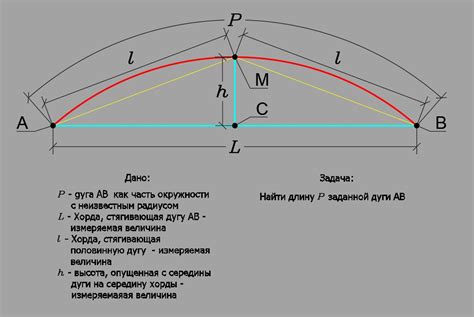
Если известны угол и длина дуги сектора окружности, то можно найти радиус данного сектора. Для этого можно использовать следующую формулу:
| Формула для нахождения радиуса |
|---|
| Радиус = Длина дуги / Угол в радианах |
Для использования формулы необходимо знать значения угла и длины дуги. Угол обычно измеряется в градусах, поэтому перед использованием формулы необходимо перевести его в радианы. Для этого нужно умножить значение угла на π/180 (где π = 3,14159 и равно отношению длины окружности к ее диаметру).
Пример:
| Угол | Длина дуги | Радиус |
|---|---|---|
| 60° | π (пи) | 1 |
| 90° | 2π (два пи) | 2 |
| 120° | 3π/2 (три пи на два) | 3/2 |
Таким образом, используя данные формулы, можно найти радиус сектора окружности, если известны угол и длина дуги.