Радиус вписанной окружности треугольника - это расстояние от центра окружности до любой из его сторон. Оказывается, радиус вписанной окружности имеет тесную связь с периметром треугольника. В этой статье мы рассмотрим, как найти радиус вписанной окружности треугольника, зная его периметр.
Перед тем, как перейти к расчетам, давайте вспомним основные понятия. Вписанная окружность треугольника - это окружность, которая касается всех трех сторон треугольника. Она имеет центр, который совпадает с центром внутренней окружности, и радиус, который называется радиусом вписанной окружности.
Окружность, вписанная в треугольник, имеет много интересных свойств и применений. Например, радиус вписанной окружности может быть использован для нахождения площади треугольника, а также для решения задач геометрической оптимизации.
Зная периметр треугольника и радиус вписанной окружности, мы можем найти все остальные параметры этого треугольника. В этой статье мы рассмотрим формулу, которая позволяет найти радиус вписанной окружности треугольника по его периметру.
Как найти радиус вписанной окружности треугольника с известным периметром
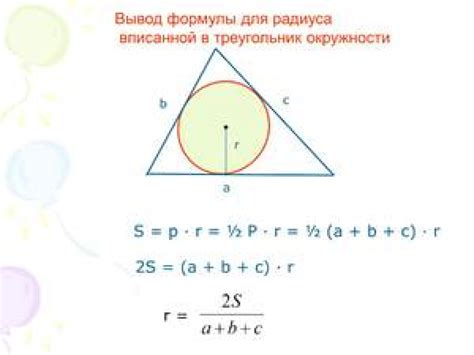
Радиус вписанной окружности треугольника представляет собой расстояние от центра окружности до любой из его сторон. Найдя радиус вписанной окружности, можно получить информацию о свойствах треугольника, таких как его площадь и углы.
Для нахождения радиуса вписанной окружности треугольника с известным периметром, можно воспользоваться следующей формулой:
| Радиус вписанной окружности (r) = | Площадь треугольника (S) | Периметр треугольника (P) |
| Полупериметр треугольника (p) = | ||
| p - сторона треугольника |
Итак, для нахождения радиуса вписанной окружности треугольника с известным периметром, нужно выполнить следующие шаги:
- Найти полупериметр треугольника (p) по формуле p = P/2.
- Найти площадь треугольника (S) по формуле Герона или другой известной формуле, используя длины сторон треугольника.
- Подставить значения полупериметра треугольника (p) и площади треугольника (S) в формулу для нахождения радиуса вписанной окружности (r).
- Выполнить необходимые вычисления, чтобы найти значение радиуса вписанной окружности треугольника.
Итак, с помощью этих простых шагов, можно найти радиус вписанной окружности треугольника с известным периметром. Знание радиуса вписанной окружности позволяет получить дополнительные данные о треугольнике и использовать их в дальнейших расчетах и изысканиях.
Преимущества изучения науки треугольника

1. Понимание геометрических принципов: Изучение науки треугольника помогает развить понимание основных геометрических принципов, таких как площадь, периметр, углы и соотношения сторон. Это позволяет более глубоко понять пространственные отношения и взаимосвязи между различными геометрическими фигурами.
2. Применение в реальной жизни: Знания в науке треугольника находят применение во многих сферах, таких как архитектура, инженерия, строительство и геодезия. Правильное применение геометрии треугольников помогает решать различные практические задачи, такие как измерение расстояний, построение более устойчивых и прочных конструкций, а также определение формы и размеров объектов.
3. Развитие логического мышления: Изучение науки треугольника требует анализа и логического мышления. Студентам приходится решать различные геометрические задачи и применять логику для поиска правильных решений. Это способствует развитию абстрактного мышления, умению анализировать и решать сложные проблемы.
4. Подготовка к высшей математике: Знание науки треугольника является базовым и необходимым для изучения более сложных математических дисциплин, таких как тригонометрия, геометрия на плоскости и в пространстве, алгебра и анализ. Основы геометрии треугольников помогут студентам лучше понять эти предметы и более успешно изучать их.
Изучение науки треугольника имеет множество преимуществ, которые расширяют кругозор студента, развивают его умственные способности и подготавливают для удаленных областей науки и техники.