Радиус вписанной окружности – это важный параметр, определяющий особенности треугольника и связанный с его сторонами и углами. Взаимосвязь между радиусом вписанной окружности и сторонами прямоугольного треугольника может быть выведена с помощью геометрических доказательств.
Для начала, давайте вспомним, что такое прямоугольный треугольник. Это треугольник, у которого один из углов равен 90 градусам. Опирающаяся на прямой угол сторона называется гипотенузой, а две оставшиеся стороны – катетами. Окружность, вписанная в прямоугольный треугольник, касается всех трех его сторон.
Чтобы найти радиус вписанной окружности в прямоугольный треугольник, нам понадобятся формулы для вычисления его площади и полупериметра. Зная площадь и полупериметр, мы можем найти радиус окружности с помощью стандартной геометрической формулы.
Вычисление радиуса вписанной окружности в прямоугольном треугольнике является важным шагом при решении задач на нахождение площади, объема и других параметров этого треугольника. Правильное использование формул и проведение доказательств позволяют установить точные значения и правильные связи между различными сторонами и углами этого треугольника.
Что такое радиус вписанной окружности в прямоугольный треугольник?
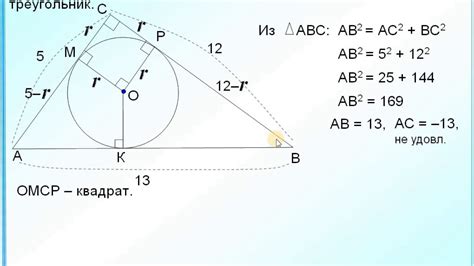
В прямоугольном треугольнике, который имеет один прямой угол (90 градусов), существует особенное свойство: вписанная окружность, которая касается всех трех сторон треугольника, имеет центр, который находится в точке пересечения медиан треугольника.
Медианы треугольника - это линии, соединяющие вершину треугольника с серединами противоположных сторон. Таким образом, радиус вписанной окружности в прямоугольный треугольник равен половине длины медианы, которая соединяет вершину прямого угла с серединой противоположной стороны.
Используя свойства прямоугольного треугольника и окружностей, можно расчитать радиус вписанной окружности и использовать его для различных математических вычислений и построений, связанных с прямоугольным треугольником.
| Свойства радиуса вписанной окружности в прямоугольный треугольник: |
|---|
| 1. Радиус вписанной окружности делит медиану треугольника на две равные части. |
| 2. Радиус вписанной окружности перпендикулярен каждой стороне треугольника, касающейся окружности. |
| 3. Радиус вписанной окружности является лучшим приближением прямой угол треугольника. |
Геометрия прямоугольного треугольника и его свойства
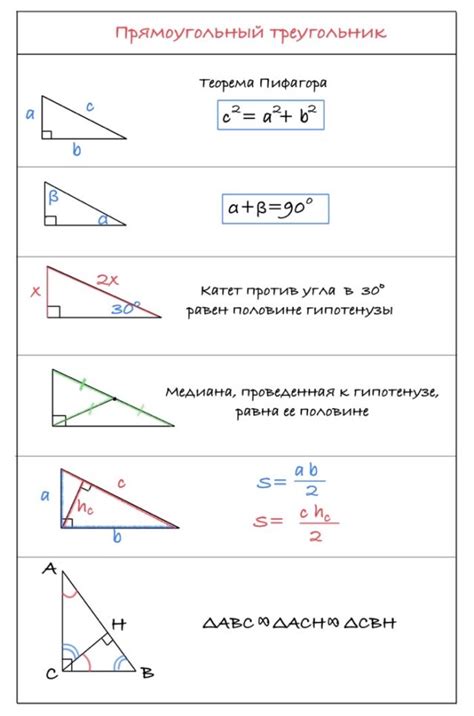
Основные свойства прямоугольного треугольника:
- Теорема Пифагора: В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Это одно из самых известных и полезных свойств прямоугольного треугольника.
- Углы прямоугольного треугольника: В прямоугольном треугольнике два острых угла суммируются до 90 градусов. Это означает, что один острый угол является дополнительным к другому острым углу.
- Высота: Высота прямоугольного треугольника - это отрезок, который проведен из вершины прямого угла (противолежащая гипотенузе) до основания (на противоположной стороне). Высота является одним из важных параметров прямоугольного треугольника и используется, например, для вычисления площади.
- Медиана: Медиана прямоугольного треугольника - это отрезок, соединяющий середину гипотенузы с противоположным острым углом. Медиана делит гипотенузу пополам, а также является высотой и биссектрисой прямоугольного треугольника.
- Вписанная окружность: В прямоугольном треугольнике, радиус вписанной окружности равен половине гипотенузы, а центр окружности совпадает с серединой гипотенузы. Вписанная окружность касается всех сторон треугольника.
Прямоугольные треугольники имеют множество других свойств и формул, которые могут быть использованы для решения геометрических задач и простых вычислений.
Заключение: Изучение свойств прямоугольного треугольника очень важно не только для геометрии, но и для практического применения в различных сферах, таких как инженерия, архитектура и физика. Понимание геометрии прямоугольного треугольника поможет вам решать задачи, находить значения сторон и углов, и применять их в реальных ситуациях.
Определение радиуса вписанной окружности
Радиус вписанной окружности в прямоугольный треугольник можно определить, зная длины его сторон.
Для начала, найдем площадь треугольника по формуле: S = (a * b) / 2, где a и b - катеты треугольника.
Затем, найдем полупериметр треугольника по формуле: p = (a + b + c) / 2, где с - гипотенуза треугольника.
И наконец, вычислим радиус вписанной окружности по формуле: r = S / p, где S - площадь треугольника, p - полупериметр треугольника.
Таким образом, зная длины сторон прямоугольного треугольника, мы можем легко определить радиус вписанной окружности.
Формула для вычисления радиуса вписанной окружности
Радиус вписанной окружности в прямоугольный треугольник можно вычислить по следующей формуле:
- Найдите полупериметр треугольника (сумма всех его сторон, деленная на 2).
- Вычислите площадь треугольника по формуле Герона.
- Радиус вписанной окружности равен площади треугольника, деленной на полупериметр треугольника.
Формула для вычисления площади треугольника по формуле Герона:
- Найдите полупериметр треугольника, как указано выше.
- Вычислите площадь треугольника по формуле Герона:
- Суммируйте квадраты длин всех сторон треугольника.
- Умножьте полученную сумму на разность полупериметра треугольника и длин каждой из его сторон.
- Вычислите квадратный корень из полученного значения.
- Площадь треугольника равна полученному значению, деленному на 4.
Пользуясь этими формулами, вы сможете точно вычислить радиус вписанной окружности в прямоугольный треугольник, что позволит вам провести точную построительную работу или осуществить геометрические расчеты.
Доказательство формулы для радиуса вписанной окружности
- Выберем в прямоугольном треугольнике один из острых углов, например, угол A.
- Построим биссектрису этого угла, которая будет являться радиусом вписанной окружности.
- Рассмотрим треугольник, образованный биссектрисой, высотой, проведенной к гипотенузе, и половиной гипотенузы. Обозначим высоту как h, половину гипотенузы как p, а радиус вписанной окружности как r.
- По свойствам треугольника можно выразить отрезки h и r через стороны треугольника и угол A:
h = p * tan(A/2)
r = p - h
- Подставим значение h во второе уравнение и получим:
r = p - p * tan(A/2)
- Упростим полученное выражение:
r = p * (1 - tan(A/2))
- Учитывая, что tan(A/2) = (1 - cos(A))/sin(A), получаем окончательную формулу для радиуса вписанной окружности в прямоугольный треугольник:
r = p * (1 - (1 - cos(A))/sin(A)) = p * (1 - (1 - sin(A))/(2*sin(A))) = p * (sin(A)/2)
Таким образом, радиус вписанной окружности в прямоугольный треугольник можно выразить через полупериметр треугольника и синус угла при прямом угле: r = p * (sin(A)/2).
Связь радиуса вписанной окружности с сторонами и площадью прямоугольного треугольника
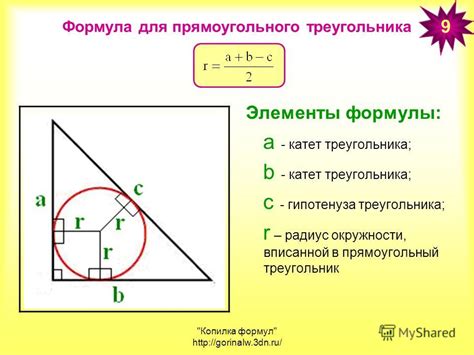
В прямоугольном треугольнике, у которого катеты равны a и b, а гипотенуза равна c, можно найти радиус r вписанной окружности. Также можно использовать площадь треугольника S.
Известно, что вписанная окружность треугольника касается всех его сторон внутренним образом. Поэтому можно сказать, что радиус вписанной окружности является расстоянием от центра окружности до каждой из сторон треугольника. Это расстояние равно пополам суммы длин катетов треугольника минус гипотенуза:
r = (a + b - c) / 2
Также радиус вписанной окружности может быть выражен через площадь треугольника. Известно, что площадь треугольника равна половине произведения длины гипотенузы на сумму длин катетов:
S = (a * b) / 2
Используя формулу для площади треугольника, можно выразить радиус вписанной окружности следующим образом:
r = √(S * 2) / (a + b + c)
| Формула для радиуса вписанной окружности: | Формула для радиуса вписанной окружности через площадь треугольника: |
|---|---|
| r = (a + b - c) / 2 | r = √(S * 2) / (a + b + c) |
Используя эти формулы, можно вычислить радиус вписанной окружности для любого прямоугольного треугольника, зная его стороны и/или площадь.
Примеры вычисления радиуса вписанной окружности в прямоугольном треугольнике

Метод нахождения радиуса вписанной окружности в прямоугольном треугольнике основан на использовании известных свойств таких треугольников. Найдем несколько примеров, чтобы более понятно разобраться в этом методе.
Пример 1:
Рассмотрим прямоугольный треугольник ABC, в котором гипотенуза AC равна 10 см, а катеты AB и BC равны 6 см и 8 см соответственно.
Для начала вычислим периметр треугольника ABC, используя формулу:
периметр = AB + BC + AC
периметр = 6 см + 8 см + 10 см = 24 см
Затем найдем полупериметр треугольника ABC, используя формулу:
полупериметр = периметр / 2
полупериметр = 24 см / 2 = 12 см
Далее вычислим площадь треугольника ABC, используя формулу Герона:
площадь = √(полупериметр * (полупериметр - AB) * (полупериметр - BC) * (полупериметр - AC))
площадь = √(12 см * (12 см - 6 см) * (12 см - 8 см) * (12 см - 10 см))
площадь = √(12 см * 6 см * 4 см * 2 см) = √(576 см²) = 24 см²
И, наконец, найдем радиус вписанной окружности по формуле:
радиус = площадь / полупериметр
радиус = 24 см² / 12 см = 2 см
Пример 2:
Рассмотрим другой прямоугольный треугольник XYZ, в котором гипотенуза XZ равна 8 см, а катеты XY и YZ равны 5 см и 7 см соответственно.
Аналогично примеру 1, вычислим периметр треугольника XYZ:
периметр = XY + YZ + XZ = 5 см + 7 см + 8 см = 20 см
Затем найдем полупериметр:
полупериметр = 20 см / 2 = 10 см
Вычислим площадь треугольника XYZ:
площадь = √(10 см * (10 см - 5 см) * (10 см - 7 см) * (10 см - 8 см))
площадь = √(10 см * 5 см * 3 см * 2 см) = √(300 см²) ≈ 17.32 см²
И, наконец, найдем радиус вписанной окружности:
радиус = 17.32 см² / 10 см ≈ 1.73 см
Таким образом, примеры показывают, как вычислить радиус вписанной окружности в прямоугольном треугольнике, используя известные свойства и формулы для периметра, полупериметра, площади и радиуса вписанной окружности. Эти вычисления могут применяться для нахождения радиуса вписанной окружности в любом прямоугольном треугольнике.
Геометрическая интерпретация радиуса вписанной окружности в прямоугольном треугольнике
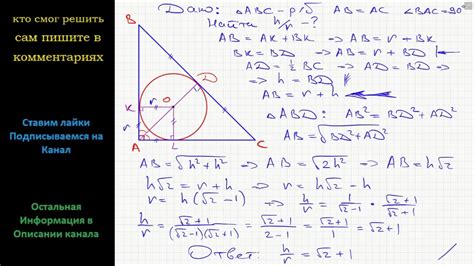
Рассмотрим прямоугольный треугольник ABC, где AB - гипотенуза, а AC и BC - катеты. Пусть O - центр вписанной окружности, а r - радиус этой окружности.
Известно, что радиус вписанной окружности перпендикулярен касательной. Также, точка касания делит касательную на два равных отрезка, обозначим их как p.
Таким образом, у нас получается, что OA = OB = p, а OC = r. Отрезок OA перпендикулярен AC и делит его на две равные части. Поэтому OA является медианой треугольника ABC.
Зная, что медиана треугольника является половиной гипотенузы, мы можем записать следующее:
OA = OB = 1/2 * AB = 1/2 * (AC^2 + BC^2)^0.5
Также, используя теорему Пифагора, можем записать:
AC^2 + BC^2 = AB^2
Подставляя это значение в предыдущее уравнение, получаем:
OA = OB = 1/2 * AB = 1/2 * AB = 1/2 * (AB^2)^0.5 = 1/2 * (AC^2 + BC^2)^0.5
Таким образом, радиус вписанной окружности прямоугольного треугольника равен половине гипотенузы, то есть:
r = 1/2 * AB = 1/2 * (AC^2 + BC^2)^0.5
Данная формула позволяет найти радиус вписанной окружности в прямоугольном треугольнике на основе длин его катетов.
Метод нахождения радиуса вписанной окружности в прямоугольном треугольнике с помощью формулы
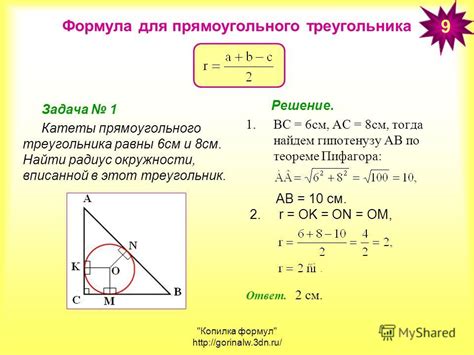
Для нахождения радиуса вписанной окружности в прямоугольном треугольнике можно использовать специальную формулу, основанную на длинах сторон треугольника. Данный метод позволяет найти радиус точно, без необходимости проводить сложные геометрические построения.
Формула для определения радиуса вписанной окружности в прямоугольном треугольнике выглядит следующим образом:
r = (a + b - c) / 2
Где:
- r - радиус вписанной окружности
- a, b - длины катетов треугольника
- c - длина гипотенузы треугольника
Для применения данной формулы необходимо знать значения длин сторон треугольника. Длины катетов можно измерить с помощью линейки или найти их значения в условии задачи. Длину гипотенузы также можно найти по теореме Пифагора, если известны длины катетов.
Найденный радиус окружности позволяет определить такие параметры, как площадь и длины сторон треугольника, а также может быть использован для дальнейших геометрических вычислений и построений.
Практическое применение радиуса вписанной окружности в прямоугольном треугольнике
Одно из применений радиуса вписанной окружности заключается в вычислении площади прямоугольного треугольника. Площадь прямоугольного треугольника можно вычислить, зная длины его сторон и радиус вписанной окружности. Формула для вычисления площади прямоугольного треугольника с использованием радиуса вписанной окружности имеет вид: S = r * p, где S - площадь треугольника, r - радиус вписанной окружности, p - полупериметр треугольника.
Другим применением радиуса вписанной окружности является вычисление длины сторон прямоугольного треугольника. Длины сторон прямоугольного треугольника могут быть выражены через радиус вписанной окружности по формуле: a = 2 * r * cos(alpha), b = 2 * r * cos(beta), c = 2 * r * cos(gamma), где a, b, c - длины сторон треугольника, r - радиус вписанной окружности, alpha, beta, gamma - углы треугольника.
Третьим применением радиуса вписанной окружности является вычисление углов прямоугольного треугольника. Углы прямоугольного треугольника могут быть выражены через радиус вписанной окружности по формуле: alpha = arcsin(a / (2 * r)), beta = arcsin(b / (2 * r)), gamma = arcsin(c / (2 * r)), где alpha, beta, gamma - углы треугольника, a, b, c - длины сторон треугольника, r - радиус вписанной окружности.
Таким образом, радиус вписанной окружности в прямоугольном треугольнике имеет практическое применение при вычислении площади треугольника, длин сторон треугольника и углов треугольника. Познание этих формул и умение применять их позволит решать различные практические задачи, связанные с прямоугольным треугольником и вписанной в него окружностью.