Равносторонний треугольник является одним из самых интересных геометрических фигур. Увидев его, мы сразу вспоминаем, что все его стороны равны, а углы при основании равны 60 градусам. Однако, мало кто знает, что в равностороннем треугольнике можно найти также радиус вписанной окружности. Именно об этом мы сегодня и поговорим.
Радиус вписанной окружности является расстоянием от центра окружности до любой точки на ее окружности. В равностороннем треугольнике радиус вписанной окружности будет проходить через середины сторон треугольника. Это значит, что чтобы найти радиус, нам нужно знать только длину одной стороны равностороннего треугольника.
Для расчета радиуса вписанной окружности в равносторонний треугольник по длине одной его стороны, мы можем использовать следующую формулу: радиус = сторона треугольника / (2 * √3), где √3 - корень из трех. Упростив эту формулу, мы получим более понятное выражение: радиус = сторона треугольника / (√3 * 2).
Таким образом, чтобы найти радиус вписанной окружности в равносторонний треугольник, нужно знать длину одной его стороны. Она будет выражаться в любых единицах измерения длины, будь то сантиметры, метры или дюймы. Просто подставьте значение стороны треугольника в формулу и получите радиус. Теперь у вас есть секрет расчета!
Как найти радиус вписанной окружности в равносторонний треугольник
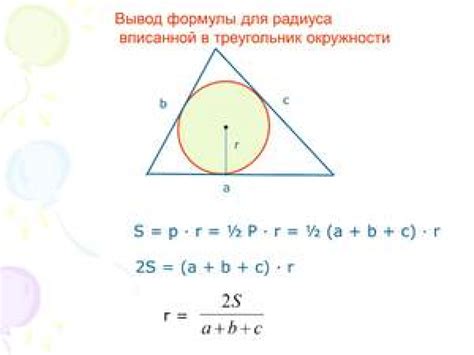
Радиус вписанной окружности в равностороннем треугольнике - это расстояние от центра окружности до любой из его сторон. Чтобы найти его, можно использовать формулу:
- Радиус вписанной окружности = (сторона треугольника)/2 * √3
Другой способ найти радиус вписанной окружности в равностороннем треугольнике - это используя формулу:
- Радиус вписанной окружности = (2 * Площадь треугольника) / (Периметр треугольника)
Зная любую сторону равностороннего треугольника, можно легко найти радиус вписанной окружности с помощью указанных формул.
Секреты расчета

Расчет радиуса вписанной окружности в равносторонний треугольник по известной стороне может показаться сложным заданием, но на самом деле имеет простую формулу. Следуя некоторым секретам, расчет можно сделать быстрым и точным.
Один из секретов заключается в использовании формулы:
r = a/(2*√3)
где r - радиус вписанной окружности, a - длина стороны равностороннего треугольника.
С помощью этой формулы можно получить радиус вписанной окружности, зная только длину одной стороны треугольника.
Также важно помнить о следующем секрете: стороны равностороннего треугольника равны между собой. Поэтому, если известна длина одной стороны, можно сразу же определить длину двух остальных сторон.
Для визуализации и лучшего понимания расчета, следует использовать таблицу:
| Длина стороны треугольника (a) | Радиус вписанной окружности (r) |
|---|---|
| 1 | 1/(2*√3) |
| 2 | 2/(2*√3) |
| 3 | 3/(2*√3) |
| 4 | 4/(2*√3) |
Используя эту таблицу и представленную формулу, можно легко определить радиус вписанной окружности в равностороннем треугольнике для любой известной длины стороны.
Таким образом, расчет радиуса вписанной окружности в равносторонний треугольник по стороне становится проще, если следовать секретам расчета и использовать правильные формулы.
Метод 1: Формула радиуса
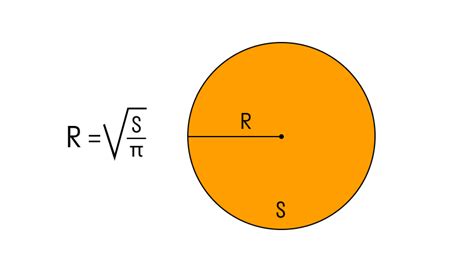
Для нахождения радиуса вписанной окружности в равносторонний треугольник по известной его стороне, можно использовать формулу, основанную на соотношении радиуса и высоты данного треугольника.
Данная формула имеет вид:
| Радиус R вписанной окружности | = | Высота данного треугольника h | / | 3 |
Таким образом, для нахождения радиуса вписанной окружности в равносторонний треугольник необходимо разделить высоту треугольника на 3.
Высоту треугольника можно найти с помощью известной стороны. Для равностороннего треугольника высота будет равна:
| Высота h | = | Сторона a | * | √ | 3 | / | 2 |
Таким образом, для рассчитывания радиуса вписанной окружности в равносторонний треугольник нужно знать только длину одной его стороны.
Используя эту формулу, вы сможете быстро и легко найти радиус вписанной окружности в равностороннем треугольнике.
Метод 2: Отношение радиуса к стороне
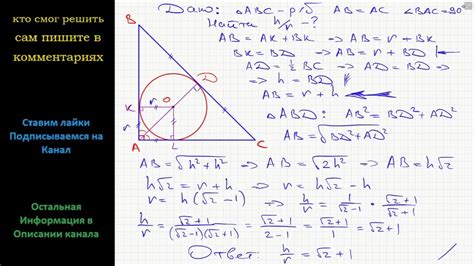
Пусть сторона равностороннего треугольника равна S. Зная формулу площади треугольника S = (sqrt(3)/4) * a^2, где a - длина стороны треугольника, можно найти значение S.
Согласно формуле площади треугольника, S = (sqrt(3)/4) * a^2. Значит, сторона равностороннего треугольника равна a = sqrt(4 * S / sqrt(3)).
Далее, используя отношение радиуса к стороне треугольника, можно найти радиус окружности R. Отношение радиуса к стороне треугольника R/a = 2/3.
Теперь можно найти радиус вписанной окружности по формуле R = (2/3) * (sqrt(4 * S / sqrt(3))).
Таким образом, используя метод отношения радиуса к стороне, можно легко и быстро найти радиус вписанной окружности в равносторонний треугольник, имея только значение длины стороны треугольника.