Сечение фигуры - это один из наиболее важных и широко используемых понятий в геометрии. Вероятно, каждый из нас сталкивался с задачами, связанными с нахождением пересечений двух или более фигур. Например, при построении дорог, планировании городов или дизайне интерьера.
Существует несколько методов, позволяющих найти сечение фигуры, но основной и наиболее распространенный метод - это алгебраический подход. Он основан на использовании уравнений, которые описывают заданные фигуры. Затем решая эти уравнения, мы можем найти точки пересечения фигур и определить их общую часть.
Кроме алгебраического подхода, существуют и другие методы, такие как геометрический подход, метод перебора и численное моделирование. Каждый из них имеет свои преимущества и недостатки, и выбор метода зависит от конкретной задачи и доступных ресурсов.
В этой статье мы рассмотрим различные методы поиска сечений фигур и предоставим примеры их практического применения. Вы узнаете, как использовать математический аппарат для нахождения сечений фигур и как применить полученные знания в реальных задачах.
Что такое сечение фигуры?

Чтобы найти сечение фигуры, мы выбираем плоскость и проводим ее через фигуру. Точки пересечения плоскости с фигурой определяют грани новой фигуры, которая является результатом сечения.
Сечение фигуры может быть полным или неполным. Полное сечение охватывает всю фигуру и может быть представлено в виде замкнутой кривой или многоугольника. Неполное сечение пересекает только часть фигуры и представляет собой искривленную линию или набор точек.
Методы и примеры нахождения сечения фигуры зависят от ее типа и геометрических особенностей. Для простых фигур, таких как круг или прямоугольник, сечение можно найти с помощью простых математических формул. Для более сложных фигур, таких как эллипс или многогранник, может потребоваться использование более сложных методов, таких как проективная геометрия или теория множеств.
| Сечение фигуры: | Результат сечения: |
 |  |
На рисунке показан пример сечения фигуры. Плоскость (пунктирная линия) пересекает фигуру (синий контур) и образует новую фигуру (зеленый контур).
Определение и основные понятия
Сечение может выполняться различными способами, в зависимости от формы и свойств данной фигуры. Например, для прямоугольника сечение может быть выполнено плоскостью, проходящей параллельно одной из его сторон, что даст в результате новый прямоугольник. Для круга сечение может быть выполнено плоскостью, проходящей через его центр и создающей новую фигуру - окружность.
Сечение фигуры может быть полным или неполным. Полное сечение охватывает всю площадь фигуры, в то время как неполное сечение охватывает только ее часть. Кроме того, сечение может быть выпуклым или вогнутым. В выпуклом сечении все точки фигуры расположены по одну сторону плоскости сечения, а в вогнутом - точки фигуры расположены по разные стороны плоскости сечения.
Для определения сечения фигуры часто используется геометрический анализ и алгоритмы. Некоторые из наиболее распространенных методов включают проекцию, пересечение и разделение фигуры плоскостью.
| Термин | Описание |
|---|---|
| Сечение | Граница или плоская поверхность, которая пересекает фигуру и создает новую фигуру. |
| Полное сечение | Сечение, охватывающее всю площадь фигуры. |
| Неполное сечение | Сечение, охватывающее только часть фигуры. |
| Выпуклое сечение | Сечение, где все точки фигуры расположены по одну сторону плоскости. |
| Вогнутое сечение | Сечение, где точки фигуры расположены по разные стороны плоскости. |
Методы нахождения сечения фигуры

Сечение фигуры позволяет определить, какая часть этой фигуры находится в определенной плоскости или продольном сечении. Существуют различные методы, позволяющие найти сечение фигуры. Вот некоторые из них:
- Метод плоского сечения. В этом методе плоскость проходит через фигуру, разделяя ее на две части. Затем определяется площадь или объем каждой из этих частей. Метод позволяет найти площадь сечения, а также определить геометрические параметры этого сечения.
- Метод цилиндрического сечения. В этом методе плоскость, параллельная оси цилиндра, проходит через фигуру, разделяя ее на две части. Затем определяется площадь или объем каждой из этих частей. Метод позволяет найти площадь сечения и определить основные параметры этого сечения.
- Метод сферического сечения. В этом методе плоскость проходит через фигуру, разделяя ее на две части. Затем определяется площадь или объем каждой из этих частей. Метод позволяет найти площадь сечения и определить основные параметры этого сечения.
- Метод пересечения. В этом методе фигура пересекается с плоскостью или другой фигурой, и в результате получается сечение. Затем определяется площадь или объем этого сечения. Метод позволяет найти площадь сечения и определить его основные характеристики.
Применение этих методов позволяет определить форму и размеры сечения фигуры, что может быть полезно при проектировании, строительстве, а также в различных научных и исследовательских задачах.
Сечение геометрических фигур
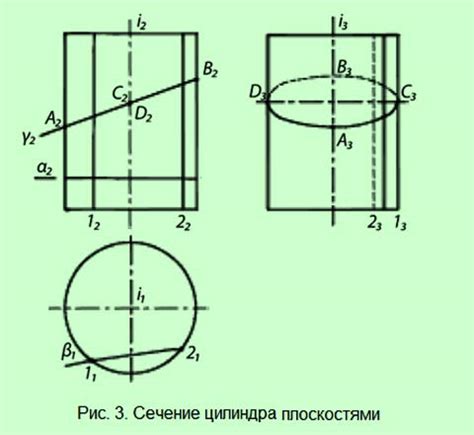
Сечение может быть полезным для определения взаимного расположения фигур, нахождения общих точек или линий, или для решения задачи на поиск пересечений. Сечение может быть проведено как в двухмерном пространстве (плоскости), так и в трехмерном пространстве (пространстве).
Сечение может быть найдено с использованием различных методов, включая геометрический анализ, алгоритмическое моделирование или методы дискретной математики. Методы могут включать построение пересечения фигур или анализ границы пересечения.
Примеры сечения геометрических фигур включают в себя нахождение пересечения двух окружностей, пересечение прямоугольника и круга, или нахождение общей области, где пересекаются несколько прямых.
Знание методов и примеров сечения геометрических фигур может быть полезно при решении задач из различных областей, таких как геометрия, физика, компьютерная графика и архитектура.
Сечение сложных фигур
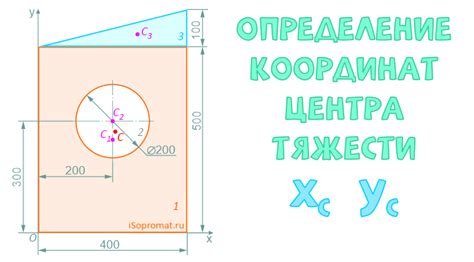
Для нахождения сечения сложной фигуры необходимо разбить ее на более простые составные части и найти сечения каждой из них. Затем, используя принцип аддитивности, суммируются площади сечений каждой составной части, чтобы получить итоговую площадь сечения.
Список методов для нахождения сечения сложных фигур может быть весьма обширным, и их выбор зависит от конкретной фигуры и задачи, которую необходимо решить. Некоторые из возможных методов включают использование геометрических формул, применение интегралов и графическое моделирование.
Одним из примеров сложной фигуры, требующей нахождения сечения, может быть сфера с отверстием внутри. В этом случае, сечение будет представлять собой две части - сферу и отверстие. Площади сечений каждой части могут быть найдены с использованием соответствующих формул для сферы и отверстия, и затем сложены вместе.
Важно помнить, что при нахождении сечения сложных фигур необходимо учесть особенности каждой составной части и правильно применить соответствующие методы и формулы.
Примеры сечения фигур
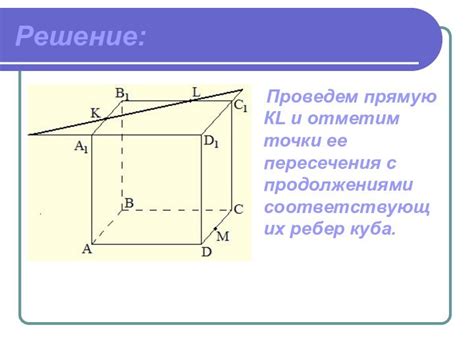
1. Сечение прямоугольника:
Пусть у нас есть прямоугольник со сторонами a = 4 см и b = 6 см. Рассмотрим сечение этого прямоугольника горизонтальной плоскостью, проходящей на половине его высоты (h = 3 см). Получится два сечения – верхнее и нижнее.
2. Сечение окружности:
Пусть у нас есть окружность радиусом r = 5 см. Разделим её на две части с помощью плоскости, проходящей через центр окружности и образующая угол 45° с диаметром. Получим две полуокружности.
3. Сечение треугольника:
Пусть у нас есть равнобедренный треугольник со сторонами a = 6 см, b = 6 см и углом при основании α = 60°. Разделим его на две части горизонтальной плоскостью, проходящей через середину высоты. Получатся два равнобедренных треугольника.
Это лишь несколько примеров сечения фигур. Применяя различные методы сечения, можно получить много интересных и полезных результатов.