Окружность - одна из самых известных и широко используемых геометрических фигур. Ее диаметр - это прямая, проходящая через центр окружности и соединяющая две ее точки на противоположных сторонах. Но что делать, если вам нужно найти сечение окружности по диаметру? В этой статье мы расскажем вам о полезных советах и методах, которые помогут вам в этой задаче.
Первым шагом для нахождения сечения окружности по диаметру является определение его координат. Если известны координаты центра окружности и длина диаметра, то можно легко найти координаты концов диаметра. Для этого необходимо разделить длину диаметра пополам и добавить/вычесть эту величину из координат центра окружности в зависимости от направления диаметра.
Однако, если вам известна только одна точка на окружности и длина диаметра, задача становится сложнее. В этом случае вам понадобится использование геометрических методов. Возможными способами являются использование квадратичных уравнений и теоремы Пифагора для нахождения координат концов диаметра. Эти методы требуют некоторых математических навыков, поэтому рекомендуется обратиться к специалисту для более точного решения задачи.
В конечном итоге, нахождение сечения окружности по диаметру может быть достигнуто различными способами. Определите, какие данные вам известны, и выберите подходящий метод для решения задачи. Запомните, что в некоторых случаях лучше обратиться к профессионалам, чтобы получить наиболее точный результат. Надеемся, что наши полезные советы и методы помогут вам достичь успеха в этой задаче!
Значение сечения окружности по диаметру
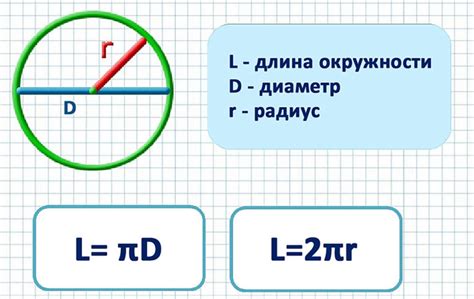
Сечение окружности по диаметру представляет собой отрезок, который разделяет окружность на две равные части. Это важное понятие, которое используется в геометрии и математике для решения различных задач.
Значение сечения окружности по диаметру можно вычислить с помощью формулы:
- Длина сечения, измеряемая в единицах длины, равна половине длины окружности.
- Площадь сечения, измеряемая в квадратных единицах, равна половине площади окружности.
Зная диаметр окружности, можно вычислить значение сечения окружности по следующим формулам:
- Длина сечения: L = π * d, где L - длина сечения, π - число Пи (приблизительно равно 3.14159), d - диаметр окружности.
- Площадь сечения: A = (π * d^2) / 4, где A - площадь сечения, π - число Пи, d - диаметр окружности.
Вычисление сечения окружности по диаметру может быть полезно во многих ситуациях, например, при решении задач по геометрии, конструировании или архитектуре. Понимание значения сечения окружности по диаметру позволяет более точно оценивать и анализировать свойства окружностей и использовать их в различных расчетах и проектировании.
Определение сечения окружности
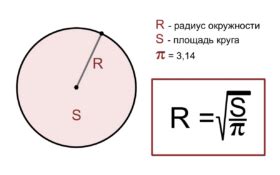
Определение сечения окружности может быть полезным для решения различных геометрических задач. Для нахождения сечения окружности по диаметру можно использовать следующий метод:
- На плоскости проводим перпендикуляр к диаметру окружности.
- С помощью циркуля или компаса отмечаем две точки на перпендикуляре, удаленные от центра окружности на равное расстояние.
- Соединяем полученные точки с концами диаметра окружности, получая тем самым сечение окружности.
Таким образом, определение сечения окружности по диаметру достаточно просто и может быть выполнено с использованием базовых геометрических инструментов.
Расчет сечения окружности по диаметру
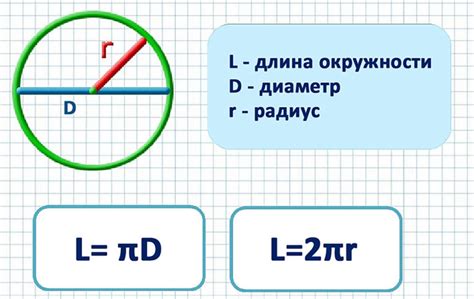
Для расчета сечения окружности по диаметру нужно знать ее диаметр. Диаметр - это отрезок, соединяющий две точки на окружности, проходя
Графическое представление сечения окружности
Один из самых простых и понятных способов представления сечения окружности - это с помощью диаграммы Венна. В этой диаграмме две окружности представляют две различные группы элементов, а пересечение окружностей показывает общие элементы этих групп.
Еще один способ графического представления сечения окружности - это с использованием геометрических фигур. Например, можно нарисовать две окружности на картоне и обрезать их таким образом, чтобы получить сечение. Это позволит наглядно представить средний участок окружности.
Другой вариант - использовать компьютерные программы для создания 3D-моделей окружности и ее сечения. Это позволяет визуализировать сечение с любым уровнем детализации и смоделировать различные углы обзора.
Графическое представление сечения окружности помогает наглядно понять ее форму и особенности, что может быть полезно при решении геометрических задач или в качестве иллюстрации в научной работе.
Применение сечения окружности в практике
- Строительство: Сечение окружности применяется при построении фундамента для зданий и сооружений, чтобы определить точку начала вращения или точку опоры. Также сечение окружности используется при создании арок и обеспечивает их точную форму.
- Дизайн: Дизайнеры мебели и предметов интерьера часто используют сечение окружности для создания эстетически привлекательных форм и деталей. Например, при создании столов или стульев форма сечения окружности может быть использована для создания удобной и эргономичной спинки или сидения.
- Машиностроение: При конструировании механизмов и машин используются детали, имеющие форму сечения окружности. Например, шкивы и зубчатые колеса имеют окружностные сечения, которые используются для передачи движения и силы.
- Космическое исследование: Сечение окружности применяется в астрономии и космическом исследовании для расчета орбит планет и спутников, а также для определения точных координат и траекторий движения космических объектов.
Это лишь некоторые примеры применения сечения окружности, которые показывают его важность в различных областях. Изучение и понимание сечения окружности является важным элементом математической и научной грамотности и может оказаться полезным во многих сферах жизни.