Сечение шара через центр круга – это плоская фигура, которая получается, если шар разрезать плоскостью, проходящей через его центр и касающейся его поверхности. Такое сечение обладает рядом интересных свойств и широко применяется в геометрии и инженерии.
Для расчета сечения шара через центр круга необходимо знать радиус данного шара и радиус круга. Формула для нахождения площади сечения выглядит следующим образом:
S = π * R^2 - π * r^2,
где S – площадь сечения, π – математическая константа, примерно равная 3,14, R – радиус шара и r – радиус круга.
Данная формула позволяет легко вычислить площадь сечения шара через центр круга и использовать полученные значения при решении различных геометрических задач. Знание данной формулы может быть полезно в архитектуре, строительстве и дизайне, где необходимо работать с трехмерными фигурами и их сечениями.
Методы определения сечения шара через центр круга
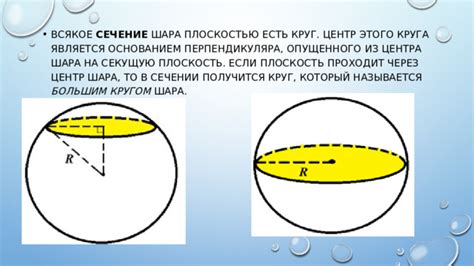
Сечение шара через центр круга представляет собой плоскую фигуру, образованную пересечением сферы и плоскости. Этот расчет часто используется в геометрии и инженерии в различных задачах, таких как расчет объемов и поверхностей, проектирование трубопроводов, конструирование радиусных столов и т.д.
Существует несколько методов определения сечения шара через центр круга. Один из самых простых методов - использование геометрических формул. Для определения площади сечения используется формула площади круга:
S = π * r^2
где S - площадь сечения, π - математическая константа (пи), r - радиус круга.
Другим методом является использование трехмерной графики и компьютерных программ. С помощью специальных программ и инструментов можно создать трехмерную модель шара и круга, затем пересечь их и вычислить площадь сечения с помощью алгоритмов.
Также существуют специальные математические функции и формулы для расчета сечения шара через центр круга. Например, можно использовать формулу площади сферического сегмента:
S = 2πrh
где S - площадь сечения, π - математическая константа (пи), r - радиус сферы, h - высота сечения.
Выбор метода определения сечения шара через центр круга зависит от конкретной задачи, доступных инструментов и предпочтений исследователя. Важно выбрать метод, который наиболее точно отражает реальность и позволяет получить необходимые результаты.
Применение формул для расчета сечения шара через центр круга

Формулы для вычисления сечения шара через центр круга находят применение в различных сферах, таких как геометрия, физика, инженерия и многое другое. Эти формулы позволяют определить площадь поверхности и объем шарового сегмента, что дает возможность анализировать пространственные фигуры и проводить различные расчеты.
Одной из основных формул, используемых для определения сечения шара через центр круга, является формула сечения плоскостью, проходящей через центр шара и круга. Для расчета площади этого сечения можно использовать следующую формулу:
A = π * r2 - h2 * (1/3) * (3 * r - h)
где A - площадь сечения;
π - математическая константа, приближенное значение которой равно 3.14159;
r - радиус шара;
h - высота шарового сегмента, измеряемая от плоскости сечения до центра шара.
Также существует формула для расчета объема шарового сегмента:
V = (π * h2 * (3 * r - h)) / 3
где V - объем шарового сегмента.
Эти формулы могут быть использованы для анализа поверхностей и объемов шаровых сегментов, что может быть полезно при проектировании и расчете различных конструкций, например, для определения объема сегмента резервуара, подводящего радиатора или других изделий, имеющих форму шара с плоскостью сечения.
Понимание и применение этих формул позволяет улучшить точность расчетов и выполнять более сложные задачи, связанные с пространственными фигурами и их характеристиками.
Обратите внимание, что для рассмотрения других типов сечений шара, таких как сечение плоскостью, не проходящей через центр, существуют другие формулы.
Практическое применение сечения шара через центр круга

Сечение шара через центр круга имеет широкое практическое применение в различных областях науки и техники. Знание формул и способов расчета позволяет решать задачи, связанные с геометрией и пространственными конструкциями.
Примером практического применения такого сечения может служить проектирование архитектурных сооружений или создание деталей и механизмов в инженерии. Например, при разработке сферических куполов или круглых панелей необходимо знать размеры и форму сечения, чтобы правильно вырезать или формовать материал.
Еще одно практическое применение сечения шара через центр круга можно найти в оптике. Оптические системы, такие как линзы, применяются в фотографии, медицине, астрономии и других областях. Форма и размеры сечения шара в таких системах имеют большое значение для достижения требуемых оптических свойств.
Также сечение шара через центр круга может быть полезным при моделировании и виртуальной реальности. Зная параметры сечения, можно создавать реалистичные трехмерные объекты и сцены, которые соответствуют принципам геометрии и физики.
В итоге, понимание и использование сечения шара через центр круга способствует развитию различных отраслей науки и техники, обеспечивая точное моделирование и расчеты, а также создание устойчивых и функциональных конструкций и систем.
Основная формула для расчета сечения шара через центр круга состоит из двух частей: нахождения угла сечения и вычисления площади сечения. Для вычисления угла сечения необходимо знать радиус круга и расстояние от центра круга до плоскости сечения. Площадь сечения вычисляется с использованием формулы площади круга и значения угла сечения.
Расчет сечения шара через центр круга может быть полезен, например, при проектировании обтекателей для автомобилей или аэродинамических профилей для самолетов. Знание площади сечения позволяет определить воздействие на объект потока воздуха, что в свою очередь может быть использовано для оптимизации дизайна и повышения эффективности движения объекта.
Важно отметить, что расчет сечения шара через центр круга является одним из множества способов анализа геометрических и физических свойств объектов. В зависимости от конкретной задачи и условий, могут использоваться и другие методы расчета и анализа.
| Формулы | Описание |
|---|---|
| Угол сечения: | θ = 2 * arcsin(d / R) |
| Площадь сечения: | S = π * R^2 * (θ - sin(θ)) |
Здесь d - расстояние от центра круга до плоскости сечения, R - радиус круга, θ - угол сечения, S - площадь сечения.