Тетраэдр - один из наиболее интересных геометрических объектов. Он имеет четыре треугольных грани и четыре вершины. Как найти сечение такого тетраэдра, заданного тремя точками? Это может быть полезно в различных областях, от архитектуры до геодезии. В этом пошаговом руководстве мы рассмотрим методику поиска сечения тетраэдра по заданным точкам.
Прежде чем приступить к поиску сечения, необходимо определить плоскость, которая будет служить нашей результирующей плоскостью сечения. Для этого мы можем воспользоваться методами векторной алгебры и геометрии. Сначала найдем нормаль к плоскости проходящей через три заданные точки с помощью векторного произведения векторов, образованных этими точками.
Затем выберем одну из трех заданных точек и подставим ее координаты в уравнение плоскости, полученное с помощью векторного произведения. Таким образом, мы получим конкретное уравнение нашей результирующей плоскости сечения. Теперь остается только найти точки пересечения нашего тетраэдра с этой плоскостью и провести через них линии, чтобы наглядно представить сечение нашего объекта.
Определяем трёхмерные координаты точек

Для определения трёхмерных координат точек, необходимо знать их положение в пространстве. Координаты точек обычно задаются тремя числами (x, y, z), где каждая координата соответствует оси x, y и z соответственно.
Чтобы определить координаты точек, можно использовать различные методы:
- Использовать измерительные инструменты (лазерный дальномер, специальные приборы) для определения точных координат.
- Использовать математические вычисления на основе известных размеров и положений других объектов.
- Если точки являются вершинами геометрической фигуры, то можно использовать информацию о размерах и форме фигуры для определения координат точек.
В случае определения трёхмерных координат точек для поиска сечения тетраэдра, требуется знать координаты всех четырёх вершин тетраэдра. Зная координаты этих точек, можно использовать их для определения параметров плоскости сечения и, таким образом, найти требуемый результат.
Убедитесь, что координаты точек указаны в правильном порядке и они соответствуют вашим требованиям и ожидаемым результатам поиска сечения тетраэдра.
Используем формулу плоскости

Чтобы найти сечение тетраэдра по трём точкам, мы можем использовать формулу плоскости. Эта формула позволяет нам определить уравнение плоскости, проходящей через заданные точки.
Для нахождения уравнения плоскости, используем следующую формулу:
| x - x0 | y - y0 | z - z0 |
|---|---|---|
| ─────── = | ─────── | ─────── |
| A | B | C |
Где (x0, y0, z0) - координаты одной из заданных точек, а A, B и C - коэффициенты, определяющие направляющие векторы плоскости.
Подставив значения координат трёх заданных точек в уравнение плоскости, мы можем получить уравнение, которое определит плоскость проходящую через эти точки. Это уравнение позволит нам найти сечение тетраэдра.
Используя формулу плоскости, мы можем найти уравнение плоскости и собрать все необходимые компоненты для нахождения сечения тетраэдра по трём точкам.
Находим нормаль вектор плоскости
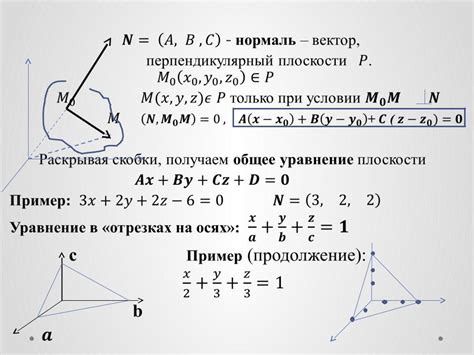
Для того чтобы найти нормаль вектор плоскости, проходящей через три заданные точки, необходимо использовать векторное произведение.
Пусть даны точки A, B и C с координатами (x1, y1, z1), (x2, y2, z2) и (x3, y3, z3) соответственно.
Нормаль вектор плоскости определяется как вектор, перпендикулярный плоскости и имеющий направление от одной из трех точек к следующей точке, против часовой стрелки.
Чтобы найти нормаль вектор плоскости, нужно вычислить векторные произведения AB и AC:
| AB: | (y2 - y1) * (z3 - z1) - (z2 - z1) * (y3 - y1) | (z2 - z1) * (x3 - x1) - (x2 - x1) * (z3 - z1) | (x2 - x1) * (y3 - y1) - (y2 - y1) * (x3 - x1) |
| AC: | (y2 - y1) * (z3 - z1) - (z2 - z1) * (y3 - y1) | (z2 - z1) * (x3 - x1) - (x2 - x1) * (z3 - z1) | (x2 - x1) * (y3 - y1) - (y2 - y1) * (x3 - x1) |
Теперь вычислим нормальный вектор плоскости, проходящей через точки A, B и C, равный:
(AB.y * AC.z - AB.z * AC.y, AB.z * AC.x - AB.x * AC.z, AB.x * AC.y - AB.y * AC.x)
Полученный вектор является нормальным вектором к плоскости.
Проверяем точку, лежит ли она на плоскости

Чтобы определить, лежит ли данная точка на плоскости тетраэдра, мы можем воспользоваться уравнением плоскости и координатами этой точки. Для этого нам необходимо вычислить значение левой части уравнения, подставив значения координат точки, и сравнить его с правой частью уравнения.
Уравнение плоскости имеет вид: Ax + By + Cz + D = 0, где x, y и z - координаты точки, A, B, C и D - коэффициенты плоскости, которые можно определить, зная тройку точек, через которые проходит плоскость.
Нам необходимо подставить значения координат точки и вычислить левую часть уравнения.
| Уравнение плоскости | Расчет левой части | Результат |
|---|---|---|
| Ax + By + Cz + D = 0 | A * x + B * y + C * z + D | Равно 0 |
Если результат вычисления равен 0, то точка лежит на плоскости тетраэдра. В противном случае, точка не лежит на плоскости и лежит вне тетраэдра.
Получаем графическое представление сечения
- Загрузите программу для 3D-моделирования, поддерживающую работу с тетраэдрами, например, Blender, 3ds Max или SolidWorks.
- Откройте программу и создайте новый проект.
- Создайте тетраэдр, используя инструменты моделирования. Для этого выберите опцию создания трёх точек и соединения их рёбрами.
- Выберите инструмент для создания плоскости с заданными основными векторами и нормалью. Введите координаты точек, полученные при поиске сечения.
- Настройте отображение сечения. В большинстве программ можно изменить цвет, прозрачность и другие параметры отображения направляющих рёбер.
- Отобразите сечение в 3D-пространстве. Убедитесь, что точки сечения находятся на плоскости. Если они смещены, проверьте правильность введённых координат.
- Рассмотрите полученное графическое представление сечения тетраэдра, чтобы визуально убедиться в его правильности и соответствии заданным точкам.