Как найти середину отрезка и разделить его на две равные части

Разделение отрезка на две равные части и поиск его середины являются основными задачами в математике и геометрии. Эти знания широко используются в различных областях, таких как инженерное дело, архитектура и программирование. В этой статье мы рассмотрим основные методы решения этой задачи.

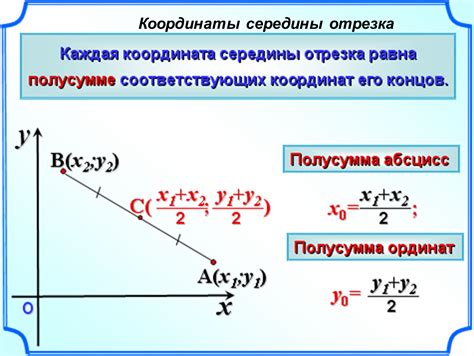
Одним из самых простых способов найти середину отрезка является применение формулы: координата середины отрезка находится как среднее арифметическое координат его концов. Если у нас есть отрезок с координатами (x1, y1) и (x2, y2), то координата x середины будет (x1 + x2) / 2, а координата y - (y1 + y2) / 2. Этот метод является быстрым и простым для реализации.

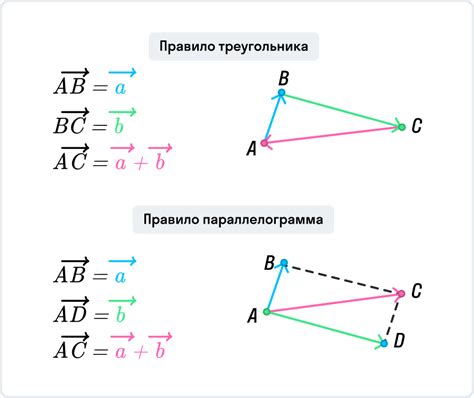
Как только мы найдем координаты середины отрезка, мы можем разделить его на две равные части с помощью векторов. Для этого мы создаем вектор v, который идет от начала отрезка до его середины (x, y). Затем мы находим координаты конца вектора v с помощью формул: x3 = x1 + (x - x1) / 2 и y3 = y1 + (y - y1) / 2. Теперь у нас есть два отрезка: (x1, y1) - (x3, y3) и (x3, y3) - (x2, y2), которые являются равными частями исходного отрезка.

Как найти середину отрезка

Найдите длину отрезка, вычтя координату начала отрезка из координаты конца отрезка.

Найдите сумму координат начала и конца отрезка.
Разделите эту сумму на 2.

Таким образом, вы получите координату середины отрезка.

Метод нахождения середины отрезка

Для нахождения середины отрезка, необходимо определить координаты начальной и конечной точек отрезка, а затем применить следующую формулу:

Середина X-координат:	`X_середина = (X_начальная + X_конечная) / 2`
Середина Y-координат:	`Y_середина = (Y_начальная + Y_конечная) / 2`

Таким образом, середина отрезка будет представлена точкой с координатами (X_середина, Y_середина).

Получив середину отрезка, его можно разделить на две равные части, найдя координаты двух новых точек. Первая точка будет иметь координаты начальной точки, а вторая точка будет иметь координаты середины отрезка.

Таким образом, мы можем решить задачу о разделении отрезка на две равные части, путем нахождения середины отрезка и определения координат новых точек.

Формула для вычисления середины отрезка

Для нахождения середины отрезка, необходимо вычислить среднее арифметическое значений его концов. Это можно сделать по следующей формуле:

Найти разность между координатами концов отрезка (x2 - x1 для оси X или y2 - y1 для оси Y).
Разделить полученную разность на 2.
Прибавить полученное значение к координате начала отрезка (x1 для оси X или y1 для оси Y).

Таким образом, после выполнения вышеуказанных шагов будет найдена середина отрезка.

Например, если у нас есть отрезок с координатами (2, 4) и (6, 8), то для нахождения его середины мы должны выполнить следующие действия:

Разность между координатами x2 - x1 = 6 - 2 = 4.
Разделить полученную разность на 2: 4 / 2 = 2.
Прибавить полученное значение к координате начала отрезка x1 + 2 = 2 + 2 = 4.

Таким образом, середина отрезка равна (4, 6).

Использование данной формулы позволяет легко и быстро находить середину отрезка и разделять его на две равные части.

Как разделить отрезок на две равные части

Если известны координаты начальной точки A(x₁, y₁) и конечной точки B(x₂, y₂), то средняя точка M(x_с, y_с) будет являться серединой отрезка AB.

Чтобы найти координаты середины отрезка, можно использовать следующие формулы:

x_с = (x₁ + x₂) / 2

y_с = (y₁ + y₂) / 2

Пример:

Пусть у нас есть отрезок AB с координатами начальной точки A(1, 2) и конечной точки B(5, 6).

Найдем середину отрезка:

x_с = (1 + 5) / 2 = 3

y_с = (2 + 6) / 2 = 4

Таким образом, середина отрезка AB будет точка M(3, 4).

Метод деления отрезка пополам

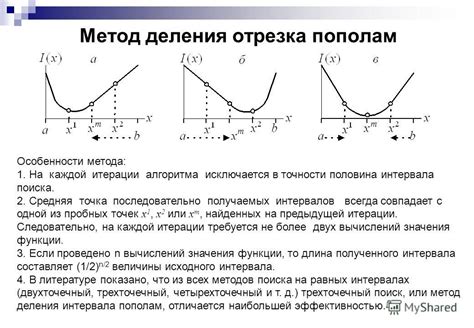
При использовании метода деления отрезка пополам, отрезок делится на две равные части путем нахождения середины отрезка. Для нахождения середины отрезка необходимо сложить координаты начальной и конечной точек отрезка и разделить полученную сумму на два.

Соответственно, середина отрезка будет находиться на равном расстоянии от начальной и конечной точек. Этот метод является простым и эффективным способом получения середины отрезка и деления его на две равные части.

Применение метода деления отрезка пополам часто встречается в задачах, связанных с определением равновесия или разделением ресурсов в равных пропорциях. Этот метод также используется в различных алгоритмах, таких как поиск бинарным разделением и бинарное дерево поиска.

Формула для вычисления точки деления отрезка

В математике для вычисления точки деления отрезка используется формула, которая позволяет найти координаты середины отрезка.

Формула для вычисления точки деления отрезка имеет вид:

x = (x₁ + x₂) / 2

y = (y₁ + y₂) / 2

где x₁ и y₁ - координаты начальной точки отрезка, x₂ и y₂ - координаты конечной точки отрезка.

Для вычисления точки деления отрезка необходимо подставить значения координат начальной и конечной точек в формулу и произвести вычисления.

Найденная точка будет являться серединой исходного отрезка.

Примеры использования

Ниже приведены несколько примеров использования алгоритма для нахождения середины отрезка и разделения его на две равные части.

Пример 1:


let startPoint = 0;
let endPoint = 10;
let middlePoint = (startPoint + endPoint) / 2;
let leftHalf = startPoint + (middlePoint - startPoint) / 2;
let rightHalf = middlePoint + (endPoint - middlePoint) / 2;
console.log(`Середина отрезка: ${middlePoint}`);
console.log(`Левая половина: ${leftHalf}`);
console.log(`Правая половина: ${rightHalf}`);

Пример 2:


let startPoint = -5;
let endPoint = 5;
let middlePoint = (startPoint + endPoint) / 2;
let leftHalf = startPoint + (middlePoint - startPoint) / 2;
let rightHalf = middlePoint + (endPoint - middlePoint) / 2;
console.log(`Середина отрезка: ${middlePoint}`);
console.log(`Левая половина: ${leftHalf}`);
console.log(`Правая половина: ${rightHalf}`);

Пример 3:


let startPoint = 1;
let endPoint = 9;
let middlePoint = (startPoint + endPoint) / 2;
let leftHalf = startPoint + (middlePoint - startPoint) / 2;
let rightHalf = middlePoint + (endPoint - middlePoint) / 2;
console.log(`Середина отрезка: ${middlePoint}`);
console.log(`Левая половина: ${leftHalf}`);
console.log(`Правая половина: ${rightHalf}`);

Если необходимо, можно изменить значения переменных startPoint и endPoint, чтобы получить середину и две равные половины для других отрезков.

Этот алгоритм особенно полезен при разделении отрезка на равные части для дальнейшего использования в различных вычислениях или алгоритмах