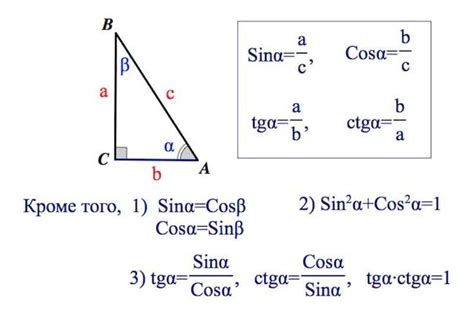
Синус - это одна из основных тригонометрических функций, которая широко используется в математике и физике. Отношение противоположной стороны к гипотенузе в прямоугольном треугольнике, синус может принимать различные значения в зависимости от угла треугольника.
В данной статье мы рассмотрим, как найти синус наименьшего угла в треугольнике. Нахождение синуса минимального угла может быть полезным при решении различных задач, например, при работе с геометрическими фигурами или при решении уравнений с тригонометрическими функциями.
Для нахождения синуса наименьшего угла можно использовать различные методы, в зависимости от доступных данных. Если даны значения двух углов треугольника, можно воспользоваться свойствами суммы углов треугольника для нахождения третьего угла, а затем применить соответствующую формулу для вычисления синуса.
Если же известны значения сторон треугольника, можно воспользоваться теоремой косинусов для нахождения всех углов треугольника, а затем выбрать наименьший угол и вычислить его синус. Этот метод особенно полезен, когда необходимо найти синус угла вне прямоугольного треугольника или в произвольном треугольнике.
Требования к знанию угла

Для того чтобы найти синус наименьшего угла, необходимо уметь определять значение угла, а также знать, что такое синус и как его вычислять. В данной статье мы подробно рассмотрим требования к знанию угла, чтобы успешно найти синус минимального угла.
Во-первых, нужно знать, что угол – это геометрическая фигура, образованная двумя лучами, исходящими из одной точки. Угол может быть измерен в градусах, радианах или градах. Для наших целей мы будем использовать градусные меры угла.
Во-вторых, для нахождения синуса угла необходимо знать определение синуса и уметь его вычислять. Синус угла можно определить как отношение противоположной стороны треугольника к гипотенузе:
| Определение | Формула |
|---|---|
| Синус угла | sin(угол) = противоположная сторона / гипотенуза |
Третье требование к знанию угла – понимание того, что синус угла может быть отрицательным, нулевым или положительным в зависимости от его квадранта. Если угол лежит в первом или во втором квадранте, то его синус будет положительным. В третьем или четвертом квадранте синус угла будет отрицательным. В случае, если угол равен 0, синус угла будет нулевым.
И последнее требование к знанию угла – умение определить наименьший угол внутри треугольника. Для этого необходимо измерить все углы треугольника и выбрать наименьший из них. Таким образом, мы сможем найти синус наименьшего угла.
Зачем нужно находить синус наименьшего угла
Знание синуса наименьшего угла полезно при решении различных задач, связанных с треугольниками. Например, для нахождения длины стороны треугольника по двум известным сторонам и углу между ними.
Поиск синуса наименьшего угла также может быть полезным при решении задач, связанных с геодезией, навигацией и оптикой. Например, при определении расстояния до объекта по его угловому размеру и известной базовой длине.
Таким образом, знание синуса наименьшего угла позволяет решать различные практические задачи, связанные с геометрией и математикой. Это незаменимый инструмент для профессионалов в области науки, инженерии и других дисциплин, где требуется работа с углами и треугольниками.
Подбор точного значения угла
При поиске синуса наименьшего угла необходимо подобрать точное значение этого угла. Для этого можно использовать различные методы и формулы.
Один из методов - использовать тригонометрические функции и их свойства. Например, можно воспользоваться тригонометрической формулой синуса двойного угла: sin(2θ) = 2sin(θ)cos(θ). Эта формула может быть полезна, если есть информация о синусе двойного угла, который можно выразить через синус наименьшего угла.
Другой способ - использовать таблицы значений тригонометрических функций. В таблицах можно найти значения синуса для различных углов и приблизительно определить значение синуса наименьшего угла.
Также можно воспользоваться калькулятором или программой, которые могут вычислить синус любого угла с большой точностью. Это наиболее точный и удобный способ найти значение синуса наименьшего угла.
Учитывая эти методы, можно подобрать точное значение угла и использовать его для нахождения синуса наименьшего угла.
Определение наименьшего угла в треугольнике

Для определения минимального угла в треугольнике необходимо знать значения всех трех углов. Используя геометрические свойства, можно найти наименьший угол, который обычно обозначается буквой "А".
Наименьший угол треугольника может быть найден по следующему алгоритму:
- Используя геометрические формулы, найдите значение всех трех углов треугольника.
- Сравните значения полученных углов и определите наименьший из них.
- Обозначьте наименьший угол буквой "А", чтобы использовать его при расчете синуса наименьшего угла.
Определение минимального угла в треугольнике важно для нахождения синуса данного угла. Синус минимального угла является важным параметром при решении задач на тригонометрию и в научных расчетах, связанных с геометрией треугольников.
Помните, что правильное определение минимального угла в треугольнике позволяет более точно выполнять вычисления и решать задачи, связанные с данной темой.
Использование геометрических фигур для определения угла
Определение наименьшего угла может быть сложной задачей, особенно если у вас нет специальных инструментов или таблиц тригонометрических функций под рукой. Однако, с помощью геометрических фигур можно сделать это задание значительно проще.
Одним из способов определить наименьший угол является использование треугольника. Вы можете нарисовать произвольный треугольник на бумаге и затем найти наименьший угол с помощью угломера или простого проведения линий.
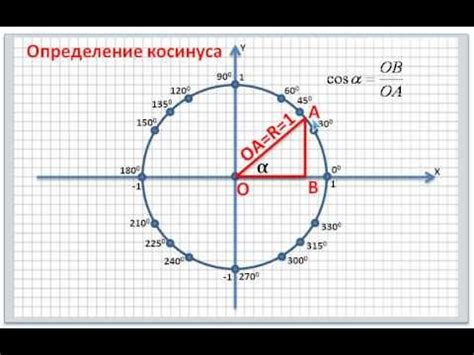
Другим методом является использование окружности. Если у вас есть окружность с центром в точке O и точкой A на периферии, вы можете провести линию от центра до точки A и найти угол между этой линией и положительным направлением оси X. Этот угол будет наименьшим.
Использование геометрических фигур для определения угла может быть полезным при решении различных задач, связанных с тригонометрией и геометрией. Оно позволяет найти синус наименьшего угла без необходимости использования сложных формул и таблиц.
Использование таблиц синусов
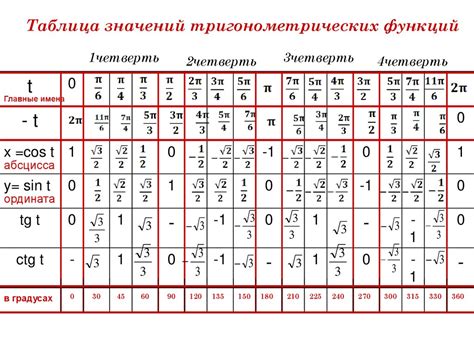
Для поиска синуса наименьшего угла можно использовать таблицы синусов. Такие таблицы содержат значения синуса для различных углов, обычно представленных в градусах или радианах.
Польза таблиц синусов заключается в том, что они позволяют быстро и удобно находить значение синуса для конкретного угла, без необходимости выполнять сложные математические вычисления.
Для использования таблицы синусов следует найти в ней значение синуса для наименьшего угла, который измеряется в градусах или радианах. Затем можно использовать найденное значение для решения задачи или дальнейших вычислений.
Таблицы синусов можно найти в учебниках математики, справочниках или онлайн ресурсах. Обычно таблица синусов представлена в виде двумерной таблицы, где значения синуса указаны для каждого угла.
Например, для нахождения синуса наименьшего угла в треугольнике можно использовать таблицу синусов, найдя в ней значение для этого угла и применив его в формуле для вычисления длины стороны треугольника. Такой подход позволяет быстро решить задачу без необходимости выполнять сложные математические операции.
Использование таблиц синусов упрощает нахождение значений синуса для различных углов и повышает точность вычислений. Однако, при работе с таблицами синусов следует быть внимательным, чтобы не допустить ошибок при чтении значений синуса из таблицы.
Отличия таблиц синусов для нахождения синуса наименьшего угла
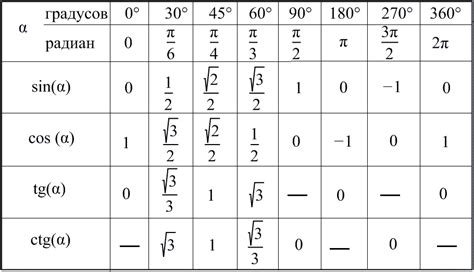
При поиске синуса наименьшего угла часто используют таблицы синусов. Однако, в зависимости от способа представления данных, таблицы могут отличаться.
В классической таблице синусов сравнивают значения синусов углов от 0° до 90°. Однако, такая таблица может быть неудобна при поиске значения синуса наименьшего угла, так как требует лишних вычислений.
- Одним из вариантов таблицы синусов для нахождения синуса наименьшего угла является таблица, где сравниваются значения синусов углов от 0° до 45°. В этой таблице синус угла наименьшего угла можно найти напрямую, без дополнительных вычислений.
- Другая вариация таблицы синусов для нахождения синуса наименьшего угла – таблица, где сравниваются значения синусов углов от 0° до 30°. При использовании этой таблицы необходимо применять дополнительные математические операции для нахождения синуса наименьшего угла.
Выбор таблицы зависит от способа решения задачи и желаемой точности ответа. Некоторые методы могут быть более удобны для определенных случаев. Например, если задача требует высокой точности, то лучше использовать полную таблицу синусов углов от 0° до 90°.
Использование таблиц синусов может значительно упростить нахождение синуса наименьшего угла и сэкономить время при выполнении задач, связанных с геометрией и тригонометрией.
Пример использования таблицы синусов
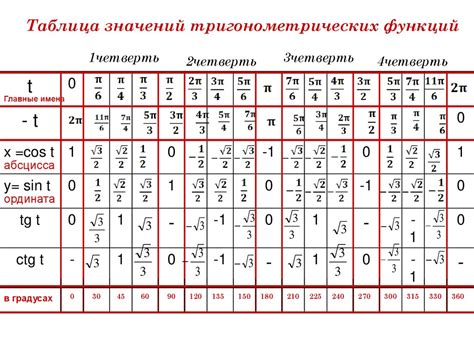
При решении задачи по нахождению синуса наименьшего угла может быть полезно использование таблицы синусов. Таблица синусов представляет собой таблицу, в которой для различных углов указаны их значения синусов.
Приведем пример использования таблицы синусов для нахождения синуса минимального угла. Предположим, что нам известен угол в градусах, для которого необходимо найти синус. Возьмем, например, угол 30 градусов.
Обратимся к таблице синусов и найдем значение синуса для угла 30 градусов. В таблице мы видим, что синус угла 30 градусов равен 0.5.
Таким образом, синус наименьшего угла, равного 30 градусов, составляет 0.5.