Синус, тангенс и котангенс - основные тригонометрические функции, которые широко используются в математике, физике и других науках. Знание этих функций позволяет решать различные задачи, связанные с измерением углов и расчетами в треугольниках.
Особенно полезным является знание способов вычисления значений тригонометрических функций при заданных значениях других функций. Например, если известен тангенс или котангенс угла, мы можем легко найти соответствующее значение синуса.
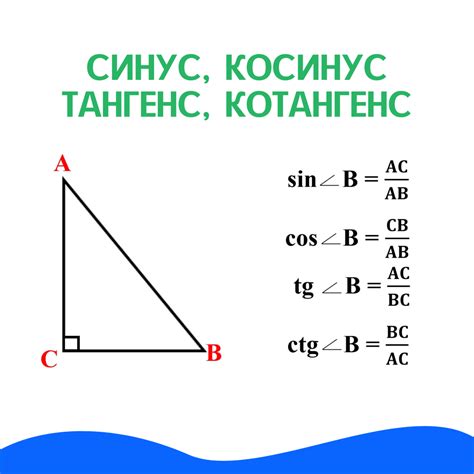
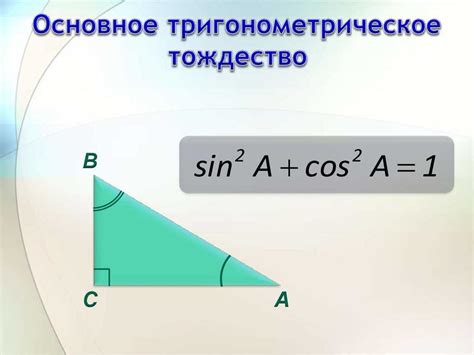
Для этого нам понадобится знание основного тригонометрического тождества, связывающего синус и косинус угла: синус равен отношению противолежащего катета к гипотенузе, а косинус равен отношению прилежащего катета к гипотенузе.
Итак, пусть у нас задан тангенс угла А, тогда мы можем использовать следующую формулу для нахождения синуса угла А: синус угла А равен отношению противолежащего катета к гипотенузе, а противолежащий катет равен синусу угла, а гипотенуза - косинусу угла. Таким образом, синус угла А можно выразить через тангенс и косинус следующим образом:
sin(A) = sin(A) = tan(A) / cos(A)
Как найти синус при известном тангенсе и котангенсе
Если известны тангенс и котангенс угла, можно использовать эти значения для нахождения синуса.
Для начала, необходимо знать, что тангенс угла равен отношению противолежащего катета к прилежащему катету, а котангенс - наоборот.
Таким образом, для вычисления синуса можно воспользоваться следующими формулами:
Если известен тангенс:
Синус = противолежащий катет / гипотенуза.
А поскольку тангенс = противолежащий катет / прилежащий катет, можно записать:
Синус = тангенс * прилежащий катет / гипотенуза.
Если же известен котангенс:
Синус = противолежащий катет / гипотенуза.
А так как котангенс = прилежащий катет / противолежащий катет:
Синус = прилежащий катет / (котангенс * противолежащий катет).
Таким образом, зная значения тангенса и котангенса, мы можем легко рассчитать синус угла.
Не забывайте, что значения тангенса и котангенса могут быть положительными или отрицательными, что может менять знак синуса. Поэтому, делайте все расчеты с учетом знака.
Простой способ расчета

Чтобы найти синус при известном тангенсе и котангенсе, можно воспользоваться простым математическим соотношением.
Сначала найдите катет, противолежащий данному углу, используя известное значение тангенса. Для этого поделите единицу на значение тангенса: катет = 1 / тангенс.
Затем найдите катет, примыкающий к данному углу, используя известное значение котангенса. Для этого поделите единицу на значение котангенса: катет = 1 / котангенс.
Используя найденные значения катетов, посчитайте гипотенузу треугольника с помощью теоремы Пифагора: гипотенуза = √(катет^2 + катет^2).
Наконец, чтобы найти синус угла, разделите найденный противолежащий катет на гипотенузу: синус = противолежащий катет / гипотенуза.
Таким образом, простым способом можно найти синус при известном тангенсе и котангенсе, используя математические соотношения и формулы. Это может быть полезно при решении различных задач и расчетах в геометрии, физике и других научных областях.
Тангенс и котангенс в геометрии
Тангенс и котангенс являются рациональными и иррациональными числами, и их значения зависят от углового измерения. Они могут быть использованы для нахождения синуса, косинуса и других тригонометрических функций, если известны значения тангенса и котангенса.
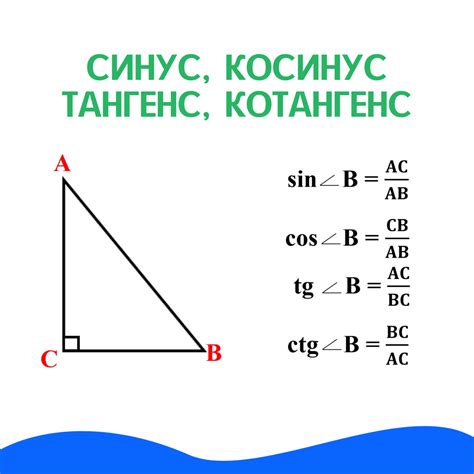
В геометрии, тангенс и котангенс находят широкое применение при определении свойств и параметров треугольников, таких как углы, стороны, площади и периметр. Они также используются для решения задач, связанных с построением и расчетами векторов.
Использование тангенса и котангенса в геометрии позволяет упростить математические вычисления и сделать их более точными. При правильном использовании этих функций можно получить более точные результаты и упростить процесс решения геометрических задач.
Соотношение тангенса и котангенса к синусу
Основным соотношением между тангенсом и синусом является:
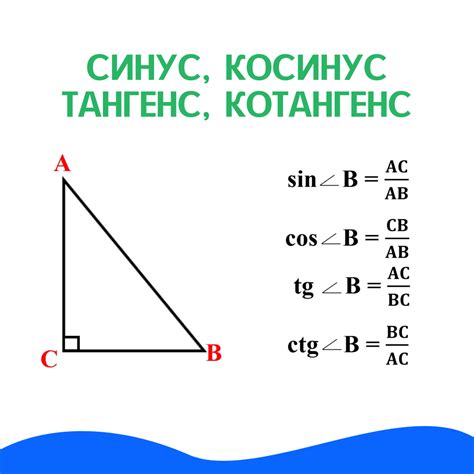
- Тангенс угла равен отношению синуса к косинусу:
tg(α) = sin(α) / cos(α).
Соотношение между синусом и котангенсом можно получить, раскрыв данное равенство:
- Тангенс угла равен обратному отношению котангенса:
tg(α) = 1 / ctg(α).
Далее, зная, что синус угла представляет собой отношение противоположной стороны к гипотенузе треугольника, можно определить соотношение между синусом и котангенсом:
- Котангенс угла равен отношению катета, противоположного данному углу, к гипотенузе треугольника:
ctg(α) = cos(α) / sin(α).
Таким образом, зная тангенс или котангенс угла, можно найти значение синуса, используя соответствующие соотношения.
Арифметический расчет тангенса и котангенса
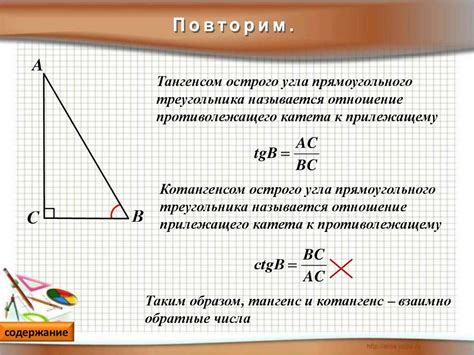
Тангенс угла определяется как отношение противолежащего катета к прилежащему, то есть: тангенс угла = противолежащий катет / прилежащий катет.
Котангенс угла определяется как отношение прилежащего катета к противолежащему, то есть: котангенс угла = прилежащий катет / противолежащий катет.
Для решения задачи про синус при известном тангенсе и котангенсе, можно воспользоваться следующими формулами:
Если известен тангенс угла, то можно найти катеты треугольника по следующим формулам:
- противолежащий катет = тангенс угла * прилежащий катет
- прилежащий катет = противолежащий катет / тангенс угла
Если известен котангенс угла, то катеты можно найти по следующим формулам:
- противолежащий катет = прилежащий катет * котангенс угла
- прилежащий катет = противолежащий катет / котангенс угла
Таким образом, зная тангенс или котангенс угла, можно легко вычислить значения противолежащего и прилежащего катетов треугольника.
Примеры расчета синуса по известному тангенсу и котангенсу
Приведем несколько примеров, чтобы проиллюстрировать, как найти значение синуса при известном тангенсе и котангенсе:
- Допустим, у нас есть задача найти синус при известном тангенсе 0,6 и котангенсе 1,66. Сначала найдем косинус по формуле: косинус = 1 / тангенс. В этом примере, косинус равен примерно 1,667. Затем найдем синус по формуле: синус = √(1 - косинус^2). В данном случае, синус составляет примерно 0,745.
- Предположим, что нам известен тангенс 1 и котангенс 0,5. Сначала найдем косинус по формуле: косинус = 1 / тангенс. В данном эксперименте, косинус равен 1. Затем найдем синус по формуле: синус = √(1 - косинус^2). Вследствие этого, синус равен 0.
- Пусть теперь тангенс равен 0,75, а котангенс равен 1,33. Последовательно найдем косинус: косинус = 1 / тангенс. В данном случае, косинус равен примерно 1,333. Затем найдем синус по формуле: синус = √(1 - косинус^2). В данной ситуации, синус составляет примерно 0,943.
Это всего лишь несколько примеров для наглядности применения формулы расчета синуса по известному тангенсу и котангенсу. Однако, вы всегда можете использовать эти формулы для любых других значений тангенса и котангенса, которые вам известны, чтобы найти значение синуса.
Значение синуса в рамках треугольников
В треугольниках с заданными углами и сторонами, синус может быть вычислен, используя другие тригонометрические отношения, такие как тангенс и котангенс. В частности:
Если известны тангенс и котангенс угла треугольника,
то синус угла может быть получен следующим образом:
sin = 1/√(1 + tg^2)
Где "tg" - это тангенс угла, а "√" - это символ для квадратного корня.
Этот простой математический способ расчета синуса позволяет нам находить значение синуса угла треугольника, используя только тангенс и котангенс. Таким образом, мы можем расширить наше понимание и использование тригонометрии в геометрии, что делает его очень полезным инструментом для решения различных задач.
Использование тангенса и котангенса для нахождения синуса

Синус угла равен отношению противолежащего катета к гипотенузе прямоугольного треугольника. То есть, sin(угол) = противолежащий катет / гипотенуза.
Тангенс угла равен отношению противолежащего катета к прилежащему. То есть, tan(угол) = противолежащий катет / прилежащий катет.
Котангенс угла равен обратному отношению тангенса. То есть, cot(угол) = 1 / tan(угол).
Для нахождения синуса угла, если известны тангенс и котангенс, можно воспользоваться следующей формулой:
sin(угол) = котангенс(угол) / √(1 + котангенс^2(угол))
Таким образом, зная значения тангенса и котангенса угла, можно вычислить его синус с помощью данной формулы и тем самым упростить расчеты в тригонометрии.