Решение геометрических задач может вызывать определенные затруднения. Особенно, если речь идет о нахождении синуса угла, образованного прямой и плоскостью. Однако, с помощью формул и подходящих алгоритмов, можно найти решение данной задачи. В этой статье мы подробно рассмотрим, как найти синус угла между прямой и плоскостью через заданные координаты.
Прежде всего, необходимо определить уравнения прямой и плоскости. Для этого используются формулы, основанные на координатах точек, через которые проходит прямая или плоскость. Затем, с помощью найденных уравнений, можно определить векторы, описывающие направление прямой и нормаль к плоскости.
Далее, используя найденные векторы, можно перейти к вычислению синуса угла между ними. Для этого применяется формула, которая основывается на скалярном произведении векторов. Результатом вычислений будет значение синуса угла. Важно отметить, что синус угла может быть положительным или отрицательным, в зависимости от расположения прямой относительно плоскости.
Итак, нахождение синуса угла между прямой и плоскостью через координаты требует использования определенных формул и алгоритмов. Однако, с правильным подходом и некоторой практикой, решение данной задачи становится возможным. Будьте внимательны при выполнении вычислений и учтите все особенности задачи, чтобы получить правильный результат.
Прямая и плоскость: определение и координаты

Когда рассматривается взаимодействие прямой и плоскости, важно знать координаты точек, через которые они проходят. Для прямой можно использовать уравнение вида y = mx + c, где m - угловой коэффициент, а c - свободный член. Для плоскости можно использовать уравнение вида Ax + By + Cz + D = 0, где A, B, C и D - коэффициенты плоскости.
Когда координаты прямой и плоскости известны, можно найти угол между ними, используя формулу sin(θ) = |ax + by + cz| / sqrt(a^2 + b^2 + c^2). В этой формуле (a, b, c) - коэффициенты плоскости, (x, y, z) - координаты точки на прямой, а | | означает модуль числа.
Зная значение синуса угла (θ) между прямой и плоскостью, можно дальше проводить геометрические и алгебраические вычисления для решения задач, связанных с этим взаимодействием.
Нахождение синуса угла между прямой и плоскостью через координаты
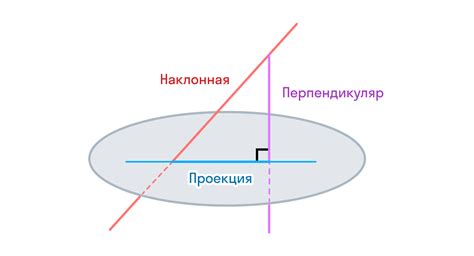
Для начала необходимо записать уравнения прямой и плоскости в трехмерном пространстве. Предположим, что уравнение прямой имеет вид:
| x - x0 | y - y0 | z - z0 |
| ––––––– = ––––––– | ––––––– = ––––––– | ––––––– = ––––––– |
| a | b | c |
где x0, y0, z0 - координаты точки на прямой, a, b, c - направляющие косинусы прямой.
Уравнение плоскости имеет вид:
| a1(x - x1) | b1(y - y1) | c1(z - z1) |
| ––––––– + ––––––– + ––––––– = 0 | ||
| a | b | c |
где x1, y1, z1 - координаты точки на плоскости, a1, b1, c1 - коэффициенты плоскости.
Для вычисления синуса угла между прямой и плоскостью необходимо найти скалярное произведение векторов, образованных направляющими векторами прямой и плоскости. После этого синус вычисляется по формуле:
синус угла = |скалярное произведение векторов| / (|прямая| * |плоскость|)
где |вектор| - длина вектора.
Таким образом, зная координаты прямой и плоскости, можно вычислить синус угла между ними.