Ромб — это геометрическая фигура, у которой все стороны равны друг другу и которая обладает некоторыми особыми свойствами. Одно из таких свойств ромба — это наличие осевой симметрии относительно его диагоналей. Для ромба также характерна наличие двух пар параллельных сторон. В геометрии, при работе с ромбом — могут возникать вопросы о нахождении разных параметров и характеристик фигуры. В этой статье мы рассмотрим, как найти синус угла ромба.
Для вычисления синуса угла ромба сначала нам понадобится знание некоторых других параметров фигуры. Для начала найдем длину его диагонали и сторону. Если известны длины диагоналей ромба, то формула для нахождения синуса угла ромба имеет вид:
sin(angle) = (2 * side) / (diagonal1 * diagonal2)
где angle — искомый угол ромба, side — длина стороны ромба, diagonal1 и diagonal2 — длины диагоналей ромба.
Рассмотрим пример. Пусть длина стороны ромба равна 5, а длины его диагоналей равны 8 и 6 соответственно. Чтобы найти синус угла ромба, подставим значения в соответствующую формулу: sin(angle) = (2 * 5) / (8 * 6). Вычислив, получим sin(angle) ≈ 0.4167. Значение синуса угла ромба округляем, можно оставить два знака после запятой. Полученный результат означает, что синус угла ромба равен примерно 0.42.
Что такое синус угла ромба?
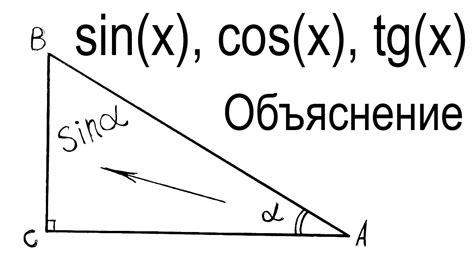
Для вычисления синуса угла ромба можно использовать специальную формулу:
| Сторона | Диагонали | |
|---|---|---|
| Синус угла ромба | sin(θ) | sin(θ/2) |
Здесь θ представляет собой величину угла ромба.
Синус угла ромба используется для решения множества задач, связанных с геометрией и тригонометрией. Например, с помощью синуса угла ромба можно определить длину стороны ромба, если известны диагонали или угол. Также этот параметр помогает вычислить высоту ромба, площадь и другие характеристики фигуры.
Зная синус угла ромба, можно легко вычислить его значение с помощью калькулятора или специальных таблиц и графиков синусов.
Формула для нахождения синуса угла ромба
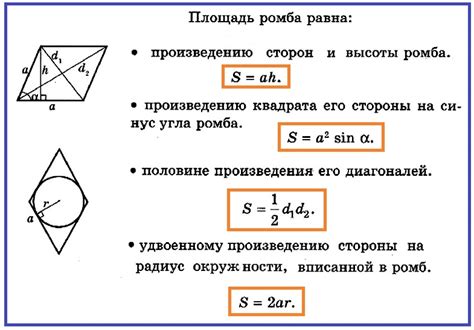
Синус угла ромба можно найти с помощью формулы:
sin(θ) = a / d
Где:
- sin(θ) - синус угла ромба;
- a - длина одного из сторон ромба;
- d - диагональ ромба.
Эта формула позволяет нам найти значение синуса угла ромба, зная длину одной из его сторон и диагональ. Синус угла ромба является отношением длины одной из его сторон к длине диагонали.
Например, если длина одной из сторон ромба равна 4 см, а диагональ равна 6 см, мы можем использовать эту формулу для нахождения синуса угла ромба:
sin(θ) = 4 / 6 = 0.6667
Таким образом, синус угла ромба равен примерно 0.6667.
Примеры вычисления синуса угла ромба
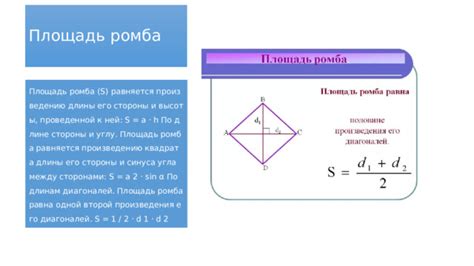
Для вычисления синуса угла ромба необходимо знать длины его сторон.
Рассмотрим несколько примеров:
Пример 1:
Сторона A ромба равна 6 см, а сторона B равна 8 см.
- Выразим синус угла через длины сторон: sin(угол) = A / B.
- Подставим известные значения: sin(угол) = 6 / 8 = 0.75.
- Синус угла равен 0.75.
Пример 2:
Сторона A ромба равна 5 см, а сторона B равна 7 см.
- Выразим синус угла через длины сторон: sin(угол) = A / B.
- Подставим известные значения: sin(угол) = 5 / 7 ≈ 0.714.
- Синус угла примерно равен 0.714.
Пример 3:
Сторона A ромба равна 9 см, а сторона B равна 12 см.
- Выразим синус угла через длины сторон: sin(угол) = A / B.
- Подставим известные значения: sin(угол) = 9 / 12 = 0.75.
- Синус угла равен 0.75.
Используя формулу вычисления синуса угла ромба, можно определить его значение в конкретных случаях, основываясь на длинах его сторон.
Значение синуса угла ромба и его особенности
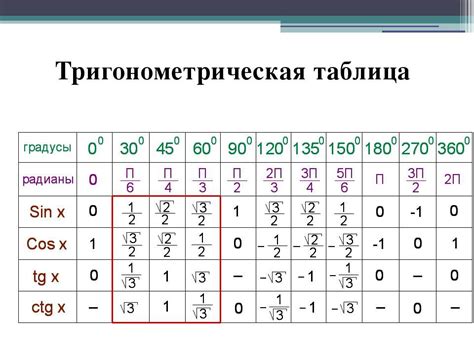
sin α = a / c
где α - угол ромба, a - длина одной из сторон ромба, c - диагональ ромба.
Зная значение синуса угла ромба, можно определить угол ромба. Для этого нужно использовать обратную функцию к синусу - арксинус (sin-1 или asin). Например, если известно, что sin α = 0.5, то арксинус от 0.5 будет равен углу α равному 30 градусов.
Одна из особенностей синуса угла ромба заключается в том, что он может принимать значения только в интервале от -1 до 1. Это связано с тем, что длина стороны ромба не может быть больше, чем диагональ, а также невозможно иметь отрицательную длину стороны или диагонали.
| Значение синуса угла α | Угол α (в градусах) |
|---|---|
| 0 | 0 |
| 0.5 | 30 |
| 0.7071 | 45 |
| 1 | 90 |
Значение синуса угла ромба часто используется при решении геометрических задач и вычислении различных параметров ромба, таких как площадь или периметр.