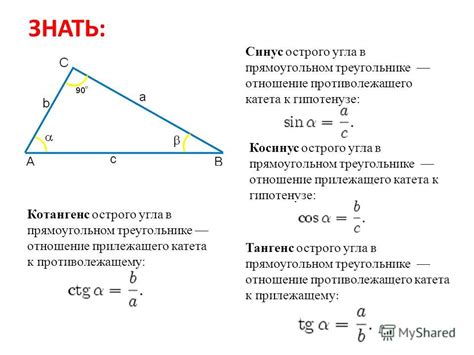
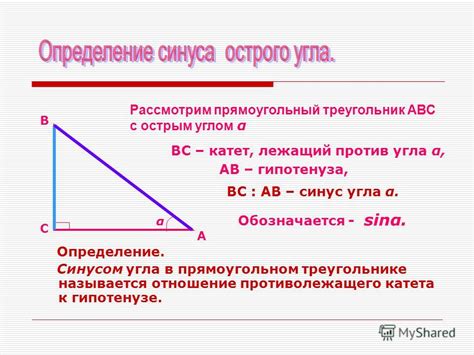
Синус угла - один из основных тригонометрических показателей, часто используемых при решении задач на геометрию и физику. Синус угла в треугольнике определяется соотношением между противоположной стороной угла и гипотенузой. Различные методы позволяют найти значение синуса угла, что помогает решить широкий спектр задач.
Для того чтобы найти синус угла, необходимо знать значения принципиальных сторон треугольника. Если известны длины двух из трех сторон треугольника, то можно воспользоваться теоремой синусов. Согласно этой теореме, отношение противоположной стороны угла к гипотенузе равно синусу этого угла.
Существует и другой метод для вычисления синуса угла в треугольнике - использование таблиц и графиков синуса. Таблица синусов предоставляет значения синуса для различных углов от 0 до 90 градусов. С помощью графика синуса можно визуально найти значение синуса угла, учитывая его величину на оси координат.
Синус угла в треугольнике - что это?
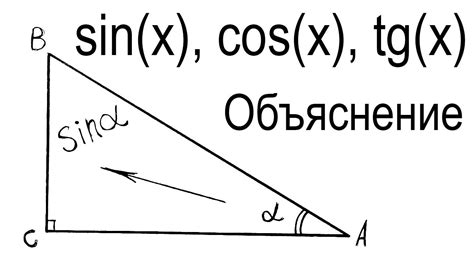
Синус угла (обозначается как sin) - это отношение: длина противоположенной стороны к длине гипотенузы. Другими словами, синус угла в треугольнике показывает, насколько длина противоположенной стороны меньше или больше гипотенузы.
Следует отметить, что синус угла в треугольнике равен отношению высоты, опущенной из вершины прямого угла к гипотенузе.
| Стороны треугольника | Определения |
|---|---|
| Гипотенуза | Самая длинная сторона треугольника, противолежащая прямому углу |
| Противоположенная сторона | Сторона, непосредственно противолежащая рассматриваемому углу |
Изучение синусов углов треугольника важно для решения задач геометрии и тригонометрии, а также для понимания принципов работы многих научных и инженерных дисциплин.
Как определить синус угла в треугольнике
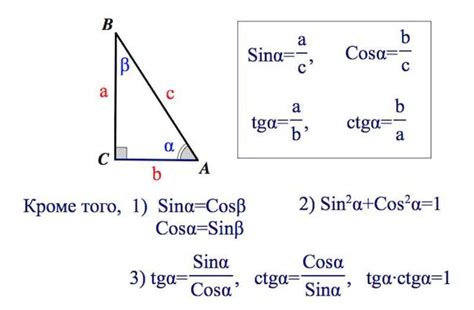
Для вычисления синуса угла необходимо знать значения длин сторон треугольника. Если известны длины сторон треугольника, можно использовать теорему синусов для вычисления синуса угла. Теорема синусов утверждает, что отношение длины стороны треугольника к синусу противолежащего угла одинаково для всех сторон и углов треугольника.
Для вычисления синуса угла можно использовать следующую формулу:
| Синус угла | = | Длина противоположного катета | / | Длина гипотенузы треугольника |
Пример:
| Длина противоположного катета (c) | = | 10 cm |
| Длина гипотенузы треугольника (h) | = | 15 cm |
Синус угла (sin A) = 10 cm / 15 cm = 0.67
Таким образом, синус угла в данном примере составляет 0.67.
Вычисление синуса угла поможет вам определить другие свойства и параметры треугольника, такие как косинус, тангенс и угол.
Формула для вычисления синуса угла в треугольнике
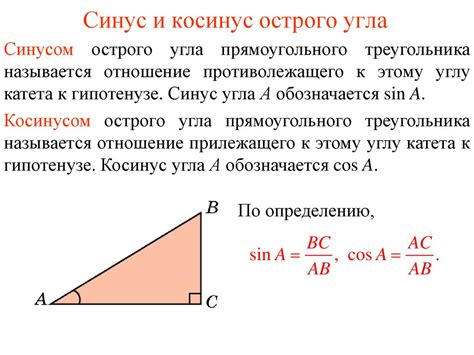
Формула для вычисления синуса угла в треугольнике выглядит следующим образом:
sin(α) = противолежащая сторона / гипотенуза
где α - угол, sin(α) - значение синуса угла, противолежащая сторона - сторона треугольника, лежащая напротив угла α, гипотенуза - сторона треугольника, являющаяся самой длинной и лежащая напротив прямого угла.
Например, если известны длины сторон треугольника и необходимо вычислить синус угла α, можно использовать формулу sin(α) = противолежащая сторона / гипотенуза и подставить соответствующие значения. Результатом будет значение синуса угла α.
Зная значения других тригонометрических функций, таких как косинус и тангенс, можно также использовать соответствующие формулы для вычисления синуса угла в треугольнике.
Пример вычисления синуса угла в треугольнике

1. Используя теорему Пифагора, найдем длину гипотенузы: АВ = √(АС² + ВС²).
2. Найдем синус угла А по формуле: sin(A) = АС / АВ.
Задан угол 30 градусов, допустим, длины сторон АС и ВС равны соответственно 4 и 6 единиц. Применяя первую формулу, получаем:
АВ = √(4² + 6²) = √(16 + 36) = √52 ≈ 7.21
Используя вторую формулу, получаем:
sin(30) = 4 / 7.21 ≈ 0.554
Таким образом, синус угла 30 градусов в этом треугольнике равен примерно 0.554.
Где используется синус угла в треугольнике
Одной из основных задач, где используется синус угла, является вычисление длин сторон треугольника. Зная значение синуса угла и длину одной из сторон, можно определить длину другой стороны с помощью тригонометрической формулы. Это особенно важно в геометрии и астрономии, где точные измерения сторон треугольников имеют большое значение для определения расстояний и углов.
Также синус угла используется для решения задач по определению высот и расстояний. Например, в геодезии с помощью синуса угла можно определить высоту небесного объекта над горизонтом или расстояние до него по известному углу наклона прибора.
Еще одной областью, где используется синус угла в треугольнике, является механика. В механике силы, действующие на тело под углом, могут быть разложены на составляющие вдоль и перпендикулярно к поверхности тела. С помощью синуса угла можно определить величину перпендикулярной составляющей силы и ее влияние на движение объекта.
Кроме того, синус угла применяется в различных инженерных расчетах, где необходимо учитывать углы наклона, например, при проектировании крыш, рамок или опорных конструкций. Знание синуса угла позволяет определить оптимальные размеры и устойчивость таких конструкций.
В итоге, знание синуса угла и умение применять его в треугольнике являются важными навыками, которые находят применение в разных областях науки, техники и повседневной жизни.
Советы при работе с синусом угла в треугольнике
При решении задач на нахождение синуса угла в треугольнике полезно следовать нескольким советам:
| 1. | Убедитесь, что у вас есть достаточно информации о треугольнике. Чтобы найти синус угла, необходимо знать длины двух сторон или стороны и высоту, либо значения всех трех сторон. | |
| 2. | Используйте соответствующее тригонометрическое соотношение. Для синуса угла в прямоугольном треугольнике, можно использовать отношение противоположного катета к гипотенузе: sin(угол) = противоположий катет / гипотенуза. Для непрямоугольного треугольника, используйте отношение соответствующих сторон или отношение стороны к длине опущенной на нее высоты. | |
| 3. | Будьте внимательны при использовании калькулятора или таблицы синусов. Убедитесь, что ваш калькулятор настроен на градусы или радианы, в зависимости от того, в чем указан угол. | |
| 4. | Не забывайте применять правило синусов. Если вам известны длины двух сторон треугольника и величина включенного угла, можно использовать следующее соотношение: сторона / sin(угол) = другая сторона / sin(другой угол). | |
| 5. | Помните о применимости теоремы Пифагора для прямоугольных треугольников. Если у вас есть прямоугольный треугольник и известны длины двух сторон, можно использовать теорему Пифагора для нахождения третьей стороны, а затем соответствующие тригонометрические соотношения для нахождения синуса угла. |
Следуя этим советам, вы сможете легко находить синус угла в треугольнике и успешно решать задачи, связанные с этой темой.