Прямоугольный треугольник – это треугольник, у которого один из углов равен 90 градусов. Он является одним из самых простых и изучаемых треугольников. Как найти стороны прямоугольного треугольника? Для этого существуют несколько формул, которые позволяют найти отсутствующие стороны при известных значениях других сторон.
Первая формула, которую можно использовать для нахождения сторон прямоугольного треугольника, называется теоремой Пифагора. Согласно этой теореме, квадрат гипотенузы (стороны, противоположной прямому углу) равен сумме квадратов катетов (двух других сторон). Формула записывается так: c^2 = a^2 + b^2, где c - гипотенуза, а и b - катеты.
Если известны значения катетов, можно легко найти гипотенузу, просто подставив значения a и b в формулу и извлекая квадратный корень: c = √(a^2 + b^2). Например, если катеты треугольника равны 3 и 4, то гипотенуза будет равна √(3^2 + 4^2) = √(9 + 16) = √25 = 5.
Как найти стороны прямоугольного треугольника

Если известны длины катетов, то можно использовать теорему Пифагора. Согласно этой теореме, квадрат гипотенузы (самой длинной стороны) равен сумме квадратов катетов. Формула для нахождения гипотенузы: c = √(a² + b²), где c – гипотенуза, a и b – катеты.
Если известна длина гипотенузы и одного из катетов, то можно использовать формулу для нахождения другого катета. Формула: b = √(c² - a²), где b – катет, c – гипотенуза, a – известный катет.
Если известны длины гипотенузы и одного из углов, можно выразить значение неизвестного катета через значение известного катета и тригонометрические функции. Формулы:
a = c * sin(α), где a – катет, c – гипотенуза, α – угол противоположный катету.
b = c * cos(α), где b – катет, c – гипотенуза, α – угол противоположный катету.
Важно помнить, что для нахождения сторон прямоугольного треугольника необходимо знать хотя бы одну из сторон или углов. Если известны две стороны или угол, можно использовать формулы для нахождения остальных сторон.
Применение данных формул позволяет находить стороны прямоугольного треугольника на практике и использовать их в решении различных задач, связанных с геометрией и строительством.
Определение прямоугольного треугольника

Прямоугольный треугольник обладает рядом особенностей. Одна из них заключается в том, что квадрат длины гипотенузы равен сумме квадратов длин катетов. Это известно как теорема Пифагора. Теорема Пифагора формулируется следующим образом:
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов:
| Теорема Пифагора |
|---|
| a2 + b2 = c2 |
Где a и b - длины катетов, c - длина гипотенузы треугольника.
Формула для нахождения гипотенузы треугольника
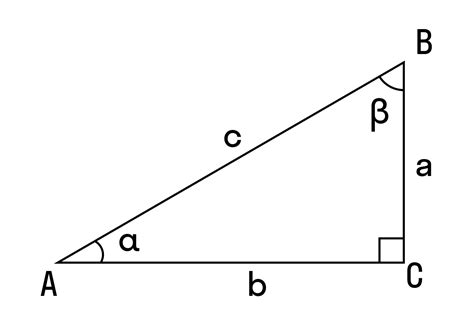
К гипотенузе прямоугольного треугольника можно применить известную теорему Пифагора. Согласно этой теореме:
- Гипотенуза равна квадратному корню из суммы квадратов катетов;
- Катеты - это две стороны прямоугольного треугольника, расположенные под прямым углом.
Формула, которую можно использовать для нахождения гипотенузы, имеет вид:
c = √(a² + b²)
Где:
- c - гипотенуза треугольника;
- a и b - катеты треугольника.
Для примера, возьмем прямоугольный треугольник со сторонами:
- Катет a = 3;
- Катет b = 4.
Подставляя значения в формулу, получим:
c = √(3² + 4²)
c = √(9 + 16)
c = √25
c = 5
Таким образом, гипотенуза треугольника равна 5.
Формула для нахождения катетов треугольника
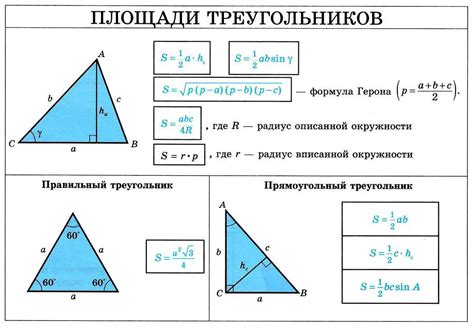
Для нахождения катетов треугольника, если известна гипотенуза и один из катетов, можно использовать теорему Пифагора:
| Катет | Гипотенуза |
|---|---|
| Катет = √(Гипотенуза² - Известный катет²) | Катет = √(Гипотенуза² - Известный катет²) |
Например, если известны гипотенуза треугольника и один из катетов, можно использовать формулу для нахождения другого катета. Допустим, у нас есть прямоугольный треугольник со сторонами: гипотенуза – 5 см и катет А – 3 см. Тогда формула будет выглядеть следующим образом:
| Катет | Гипотенуза | Известный катет |
|---|---|---|
| Катет В = √(5² - 3²) | 5 см | 3 см |
Подставив значения в формулу, получим:
| Катет В |
|---|
| Катет В = √(25 - 9) |
| Катет В ≈ √16 |
| Катет В ≈ 4 см |
Таким образом, в прямоугольном треугольнике со сторонами: гипотенуза – 5 см и катет А – 3 см, второй катет (катет В) будет примерно равен 4 см.