Прямоугольный треугольник является одной из наиболее распространенных геометрических фигур, которую можно встретить как в математике, так и в повседневной жизни. Отличительной особенностью прямоугольного треугольника является наличие одного прямого угла внутри фигуры.
Найти стороны прямоугольного треугольника с гипотенузой и углом можно с помощью нескольких формул и правил. Одним из наиболее простых и популярных способов является использование тригонометрических функций, таких как синус, косинус и тангенс.
С использованием тригонометрических функций можно выразить длины двух катетов прямоугольного треугольника через длину гипотенузы и известный угол между гипотенузой и одним из катетов. Для этого можно использовать формулы sin(угол) = противолежащий катет / гипотенуза и cos(угол) = прилежащий катет / гипотенуза.
Таким образом, зная длину гипотенузы и значение угла между гипотенузой и одним из катетов, можно выразить длины обоих катетов и найти требуемые стороны прямоугольного треугольника.
Как найти стороны прямоугольного треугольника

- 1. Найдите значение синуса или косинуса заданного угла. Для этого можно использовать таблицы значений или калькулятор.
- 2. Зная значение синуса или косинуса угла, выразите одну из сторон треугольника через гипотенузу и значение синуса или косинуса.
- 3. Используя теорему Пифагора, найдите вторую сторону треугольника. Теорема Пифагора гласит, что квадрат гипотенузы равен сумме квадратов катетов.
Итак, чтобы найти стороны прямоугольного треугольника с гипотенузой и углом, нужно использовать значения синуса или косинуса угла, гипотенузу и теорему Пифагора.
Определение прямоугольного треугольника

Гипотенуза является наибольшей стороной прямоугольного треугольника. Катеты же образуют прямой угол и всегда меньше гипотенузы.
Угол, являющийся прямым, обозначается символом ∠∅ или буквой "C".
Известная гипотенуза и угол
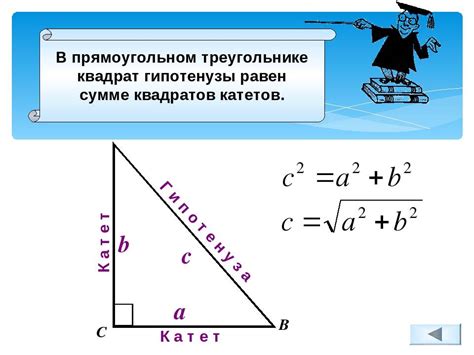
Если известны гипотенуза и угол прямоугольного треугольника, можно определить значения его катетов и составить его геометрическую модель.
Для нахождения катетов треугольника с известной гипотенузой и углом можно использовать тригонометрические функции. Например, для нахождения катета a требуется найти косинус угла α и умножить его на длину гипотенузы c:
a = c * cos(α)
Аналогично, для нахождения катета b, можно использовать тангенс угла α:
b = c * tan(α)
Используя данные формулы, можно вычислить значения катетов и построить геометрическую модель прямоугольного треугольника с известной гипотенузой и углом.
Знание данных формул позволяет решать разнообразные задачи, связанные с прямоугольными треугольниками, например, находить длину стороны прямоугольного треугольника или его площадь.
Важно помнить, что в случае прямоугольного треугольника с известной гипотенузой и углом, значения катетов всегда будут зависеть от величины угла. Поэтому при работе с такими задачами необходимо учитывать указание на единицы измерения и точность результата.
Нахождение катетов и угла
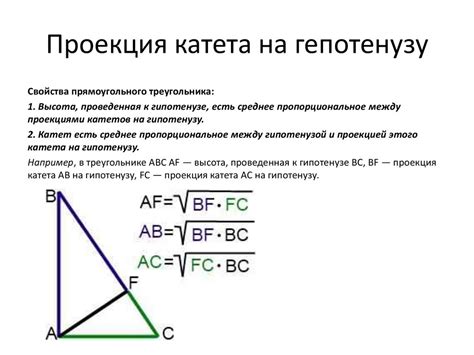
Для нахождения катетов и угла в прямоугольном треугольнике с известной гипотенузой и заданным углом, можно использовать тригонометрические функции и соответствующие формулы.
Если известны гипотенуза и один катет, то оставшийся катет можно найти с помощью функции синуса. Формула для нахождения катета:
| Известно: | Находится: |
|---|---|
| Гипотенуза (c) | Катет (a) |
a = c * sin(угол)
Если известны гипотенуза и другой катет, то оставшийся катет можно найти с помощью функции косинуса. Формула для нахождения катета:
| Известно: | Находится: |
|---|---|
| Гипотенуза (c) | Катет (b) |
b = c * cos(угол)
Если известны оба катета, то угол можно найти с помощью функции арктангенса. Формула для нахождения угла:
| Известно: | Находится: |
|---|---|
| Катет (a) | Угол (угол) |
| Катет (b) |
угол = atan(a / b)
Используя данные формулы, вы сможете находить катеты и угол в прямоугольном треугольнике с известной гипотенузой и заданным углом.
Примеры задач

Для лучшего понимания работы с гипотенузой и углами в прямоугольных треугольниках рассмотрим несколько примеров:
Пример 1:
Дан треугольник ABC, где угол B равен 90 градусов, гипотенуза AC равна 10 единиц. Найдем длину стороны AB и BC.
Решение:
Используем теорему Пифагора: AB^2 + BC^2 = AC^2.
Подставляем известные значения: AB^2 + BC^2 = 10^2.
Поскольку треугольник прямоугольный, то AB*BC/2 = S, где S - площадь треугольника. Площадь треугольника можно найти по формуле S = (AB * BC) / 2.
Теперь решим уравнение AB^2 + BC^2 = 100 и AB*BC/2 = S.
Ответ: AB ≈ 6.708 единиц, BC ≈ 8.660 единиц.
Пример 2:
Дан треугольник XYZ, где угол Y равен 90 градусов, гипотенуза XZ равна 15 единиц. Найдем длину стороны XY и YZ.
Решение:
Используем теорему Пифагора: XY^2 + YZ^2 = XZ^2.
Подставляем известные значения: XY^2 + YZ^2 = 15^2.
Поскольку треугольник прямоугольный, то XY*YZ/2 = S, где S - площадь треугольника. Площадь треугольника можно найти по формуле S = (XY * YZ) / 2.
Теперь решим уравнение XY^2 + YZ^2 = 225 и XY*YZ/2 = S.
Ответ: XY ≈ 5.831 единиц, YZ ≈ 13.228 единиц.