Геометрическая прогрессия – это числовая последовательность, в которой каждый следующий член получается умножением предыдущего на постоянное число, называемое знаменателем прогрессии.
Чтобы найти сумму геометрической прогрессии, необходимо знать первый элемент прогрессии, знаменатель и количество элементов. В данном случае, первый элемент равен 40, знаменатель равен 20/40=0.5, и прогрессия состоит из 3 элементов (40, 20, 10).
Для нахождения суммы геометрической прогрессии существует формула:
Sn = a1((qn - 1)/(q - 1)),
где Sn - сумма прогрессии, a1 - первый элемент прогрессии, q - знаменатель прогрессии, n - количество элементов прогрессии.
Подставив значения в формулу, мы получим:
S3 = 40 * ((0.53 - 1)/(0.5 - 1)) = 40 * ((0.125 - 1)/(-0.5)) = 40 * (-0.875/-0.5) = 40 * 1.75 = 70.
Таким образом, сумма геометрической прогрессии с элементами 40, 20 и 10 равна 70.
Как найти сумму геометрической прогрессии?

Sn = a1 * (1 - qn) / (1 - q),
где Sn - сумма n элементов ГП,
a1 - первый элемент ГП,
q - знаменатель ГП,
n - количество элементов ГП, для которых требуется найти сумму.
Например, для ГП со значениями 40, 20, 10 мы можем найти:
| n | Sn |
|---|---|
| 1 | 40 |
| 2 | 60 |
| 3 | 70 |
| 4 | 73.33 |
Таким образом, сумма первых 4 элементов данной ГП составляет 73.33.
Используя формулу, вы сможете легко и быстро найти сумму элементов любой геометрической прогрессии.
Что такое геометрическая прогрессия?

В геометрической прогрессии присутствуют три основных элемента:
- Первый член - начальный элемент последовательности.
- Знаменатель - число, на которое умножается каждый предыдущий элемент для получения следующего.
- Количество членов - количество элементов в последовательности.
В данной задаче, элементы геометрической прогрессии равны 40, 20 и 10. Чтобы найти сумму такой прогрессии, необходимо использовать формулу:
S = a(1 - q^n) / (1 - q),
где:
- S - сумма геометрической прогрессии;
- a - первый член прогрессии;
- q - знаменатель;
- n - количество членов прогрессии.
Подставляя значения из задачи, получаем:
S = 40(1 - 0.5^3) / (1 - 0.5) = 40(1 - 0.125) / 0.5 = 40(0.875) / 0.5 = 35 / 0.5 = 70.
Таким образом, сумма геометрической прогрессии с элементами 40, 20 и 10 равна 70.
Формула для нахождения суммы геометрической прогрессии
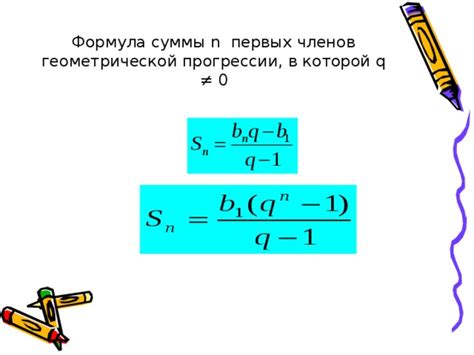
Примером геометрической прогрессии может служить последовательность 40, 20, 10, где знаменатель равен 0.5 (поскольку 20 = 40 * 0.5 и 10 = 20 * 0.5).
Сумма геометрической прогрессии может быть найдена с использованием формулы:
S = a * (1 - r^n) / (1 - r),
где:
S - сумма геометрической прогрессии,
a - первый элемент геометрической прогрессии (в данном случае 40),
r - знаменатель прогрессии (в данном случае 0.5),
n - количество элементов прогрессии.
Для примера последовательности 40, 20, 10 сумма может быть найдена следующим образом:
S = 40 * (1 - 0.5^3) / (1 - 0.5) = 80.
Таким образом, сумма геометрической прогрессии равна 80.
Какие элементы даны в геометрической прогрессии?

Данная геометрическая прогрессия имеет следующие элементы:
- Первый элемент = 40
- Второй элемент = 20
- Третий элемент = 10
Геометрическая прогрессия характеризуется тем, что каждый следующий элемент получается умножением предыдущего элемента на одно и то же число, называемое знаменателем прогрессии. В данном случае, чтобы получить следующий элемент, необходимо предыдущий элемент умножить на 0.5.
Пример: геометрическая прогрессия с элементами 40, 20, 10

В данном примере мы имеем геометрическую прогрессию с элементами 40, 20, 10. Здесь знаменатель равен 1/2. Каждый следующий элемент получается путем умножения предыдущего на 1/2.
Чтобы найти сумму геометрической прогрессии, необходимо использовать следующую формулу:
Sn = a * (1 - rn) / (1 - r)
Где:
Sn – сумма первых n элементов геометрической прогрессии;
a – первый элемент геометрической прогрессии (в данном случае 40);
r – знаменатель прогрессии (в данном случае 1/2);
n – количество элементов, сумму которых мы хотим найти (в данном случае 3).
Подставляя значения в формулу, получим:
S3 = 40 * (1 - (1/2)3) / (1 - 1/2)
Вычисляя данное выражение, получим итоговую сумму геометрической прогрессии:
S3 = 40 * (1 - 1/8) / (1 - 1/2) = 40 * (7/8) / (1/2) = 40 * 7 * 2 / 8 = 70
Таким образом, сумма геометрической прогрессии с элементами 40, 20, 10 равна 70.
Шаги для нахождения суммы геометрической прогрессии

- Определите первый член геометрической прогрессии. В данном случае первый член равен 40.
- Определите знаменатель геометрической прогрессии. Знаменатель можно найти как отношение второго члена к первому члену. В данном случае знаменатель равен 20/40, что равно 0.5.
- Определите количество элементов в геометрической прогрессии. В данном случае количество элементов равно 3.
- Используя формулу для суммы геометрической прогрессии, найдите сумму. Формула выглядит следующим образом: S = a(1 - r^n) / (1 - r), где S - сумма, a - первый член, r - знаменатель, n - количество элементов. В нашем случае: S = 40(1 - 0.5^3) / (1 - 0.5), что равно 70.
Решение: нахождение суммы геометрической прогрессии с элементами 40, 20, 10

Для нахождения суммы геометрической прогрессии необходимо знать ее начальный элемент, знаменатель и количество элементов.
В данном случае, начальный элемент равен 40, знаменатель равен половине предыдущего элемента, то есть 0.5, а количество элементов равно 3.
Используем формулу для нахождения суммы геометрической прогрессии:
Sn = a * (1 - qn) / (1 - q),
где Sn - сумма геометрической прогрессии до n-го элемента, a - начальный элемент прогрессии, q - знаменатель прогрессии, n - количество элементов.
Подставляя значения из условия, получим:
S3 = 40 * (1 - 0.53) / (1 - 0.5).
Выполняем вычисления:
S3 = 40 * (1 - 0.125) / 0.5.
S3 = 40 * 0.875 / 0.5.
S3 = 35.
Таким образом, сумма геометрической прогрессии с элементами 40, 20, 10 равна 35.