Векторы являются основой линейной алгебры и находят широкое применение в различных областях науки и техники. Для работы с векторами необходимо знать, как вычислять их координаты в различных базисах. Одним из важных заданий является нахождение суммы координат вектора в заданном базисе.
Чтобы найти сумму координат вектора, необходимо представить его в виде линейной комбинации базисных векторов. В базисе векторы играют роль координатных осей, и их комбинация позволяет определить координаты любого вектора в пространстве.
Для расчета суммы координат вектора в базисе используется метод линейной комбинации. Вначале вектор представляется в виде линейной комбинации базисных векторов, где каждому базисному вектору сопоставляется его коэффициент. Затем производится вычисление суммы произведений коэффициентов на соответствующие базисные векторы, что дает искомые координаты вектора в базисе.
Методы расчета суммы координат вектора в базисе

При работе с векторами в линейной алгебре, возникает задача нахождения суммы координат вектора в заданном базисе. В данном разделе мы рассмотрим несколько различных методов расчета данной суммы.
Метод I: Расчет суммы координат вектора в базисе может быть выполнен путем умножения каждой координаты вектора на соответствующую координату базисного вектора и последующего сложения полученных произведений. Формула для данного метода приведена ниже:
a1*b1 + a2*b2 + ... + an*bn,
где a1, a2, ..., an - координаты вектора, b1, b2, ..., bn - соответствующие координаты базисного вектора.
Метод II: Для нахождения суммы координат вектора в базисе можно использовать матричное представление. Запишем координаты вектора и базисные вектора в виде матрицы, и затем перемножим эти матрицы. Результатом будет матрица, в которой каждый элемент будет являться суммой произведений соответствующих элементов вектора и базисного вектора. Окончательная сумма будет равна сумме элементов полученной матрицы. Формула для данного метода выглядит следующим образом:
А * B = C,
где А - матрица, содержащая координаты вектора, B - матрица, содержащая координаты базисных векторов, C - результирующая матрица с суммой произведений.
Метод III: Еще одним способом решения задачи является построение системы линейных уравнений. Для этого необходимо записать координаты векторов в виде системы уравнений с неизвестными коэффициентами, после чего решить полученную систему. Результатом будет набор значений коэффициентов, каждый из которых будет соответствовать координате вектора в базисе. Сумма координат вектора будет равна сумме этих коэффициентов.
Таким образом, существуют несколько методов расчета суммы координат вектора в заданном базисе. Выбор метода зависит от конкретной ситуации и предпочтений. Рассмотренные методы обеспечивают точные и надежные результаты при выполнении математических операций с векторами в базисе.
Примеры расчета суммы координат вектора в базисе
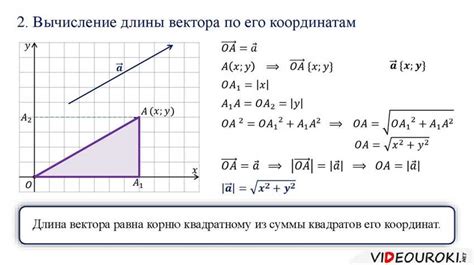
Для того чтобы найти сумму координат вектора в базисе, необходимо знать координаты вектора и базисные векторы, которые образуют данную систему.
Рассмотрим пример. Пусть дан вектор v(4, -2) и система базисных векторов b1(2, 1) и b2(-1, 3).
Для нахождения суммы координат вектора v в базисе, необходимо представить вектор v как линейную комбинацию базисных векторов и найти коэффициенты этой комбинации. Для этого составим систему уравнений:
4 = 2a - b
-2 = a + 3b
Решая данную систему уравнений, найдем коэффициенты a = 2 и b = -1.
Теперь мы можем записать вектор v как линейную комбинацию базисных векторов:
v = 2b1 - b2
Подставляя значения базисных векторов, получим:
v = 2(2, 1) - (-1, 3) = (4, 2) + (1, -3) = (5, -1)
Таким образом, сумма координат вектора v в базисе равна (5, -1).
Методы нахождения суммы координат вектора в базисе

Для нахождения суммы координат вектора в базисе существуют несколько методов. Каждый метод подходит для определенных условий и типов базиса.
Метод аналитического нахождения:
Этот метод подходит для нахождения суммы координат вектора в евклидовом пространстве с прямоугольным базисом. Он основан на разложении вектора по базисным векторам и подсчете суммы произведений координат вектора на координаты базисных векторов.
Пусть задан вектор v = (v1, v2, ..., vn) и базисные векторы e1, e2, ..., en. Тогда сумма координат вектора v в базисе будет равна:
v = v1 * e1 + v2 * e2 + ... + vn * en
Метод геометрического нахождения:
Этот метод подходит для нахождения суммы координат вектора в геометрическом пространстве с базисом, заданным точками. Он основан на геометрических свойствах векторов и требует наличия информации о длинах и углах между базисными векторами.
Пусть задан вектор v и базисные векторы e1, e2, ..., en. Тогда сумма координат вектора v в базисе будет равна проекции вектора v на каждый из базисных векторов, умноженным на длину этого вектора. Сумма проекций будет равна сумме координат вектора в базисе.
Метод матричного нахождения:
Этот метод подходит для нахождения суммы координат вектора в линейном пространстве с базисом, заданным матрицей. Он основан на матричных операциях и требует наличия матрицы перехода от базиса к стандартному базису.
Пусть задан вектор v и матрица перехода P от базиса к стандартному базису. Тогда сумма координат вектора v в базисе будет равна произведению матрицы P на вектор v.
Выбор метода для нахождения суммы координат вектора в базисе зависит от условий задачи, доступных данных и типа базиса. Каждый метод имеет свои преимущества и ограничения, и выбор метода должен быть обоснован и обусловлен контекстом задачи.
Алгоритмы расчета суммы координат вектора в базисе

Существует несколько алгоритмов, которые позволяют рассчитать сумму координат вектора в базисе.
1. Алгоритм перевода координат вектора в новый базис. В этом алгоритме необходимо сначала найти матрицу перехода от исходного базиса к новому базису. Затем умножить вектор координат исходного вектора на матрицу перехода, получив вектор координат в новом базисе. Затем сложить все координаты полученного вектора и получить сумму.
2. Алгоритм суммирования координат поэлементно. В этом алгоритме необходимо сложить каждую пару соответствующих координат исходного вектора и базиса. Например, если исходный вектор задан в формате (x1, y1, z1), а базис представлен векторами (a1, b1, c1), (a2, b2, c2), (a3, b3, c3), то сумма координат будет равна (x1 * a1 + y1 * b1 + z1 * c1) + (x1 * a2 + y1 * b2 + z1 * c2) + (x1 * a3 + y1 * b3 + z1 * c3).
3. Алгоритм использования координат вектора в базисе. В этом алгоритме сумма координат вектора в базисе вычисляется путем простой суммирования всех координат исходного вектора в базисе. Для этого нужно просто сложить все числа, заданные в координатах вектора в базисе.
Выбор конкретного алгоритма зависит от задачи и удобства использования. Предпочтительно использовать алгоритм, который подходит под конкретные требования и обеспечивает точность и эффективность расчетов.