Геометрическая прогрессия – это последовательность чисел, в которой каждый следующий элемент получается умножением предыдущего элемента на постоянное число, называемое знаменателем прогрессии. Определение суммы шести чисел геометрической прогрессии может быть полезным во многих задачах, начиная от финансовых расчетов и заканчивая научными исследованиями.
Для нахождения суммы шести чисел геометрической прогрессии используется формула суммы первых n членов прогрессии. Для нахождения суммы шести чисел геометрической прогрессии нужно знать первый элемент прогрессии, знаменатель прогрессии и количество элементов n. Зная эти три параметра, можно приступить к расчету суммы и получить нужный результат.
Давайте рассмотрим пример. Пусть первый элемент геометрической прогрессии равен 2, знаменатель прогрессии равен 3 и нас интересует сумма первых шести элементов. Используя формулу суммы геометрической прогрессии, получим следующий результат:
S = a * (1 - q^n) / (1 - q)
Вставляя значения из нашего примера, получаем:
S = 2 * (1 - 3^6) / (1 - 3)
После вычислений получим окончательный результат суммы первых шести чисел геометрической прогрессии. Этот результат будет полезен при решении конкретных задач, требующих нахождения суммы геометрической прогрессии.
Определение геометрической прогрессии и ее особенности
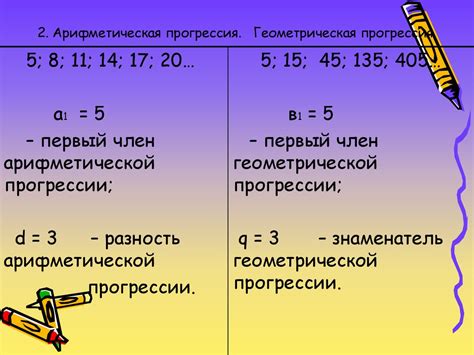
Особенности геометрической прогрессии:
- Знаменатель прогрессии отличен от нуля;
- Первый элемент (a1) задан;
- Числа образующие геометрическую прогрессию называются ее членами;
- Число элементов прогрессии может быть как конечным, так и бесконечным;
- Если |знаменатель прогрессии| 1, прогрессия будет возрастающей.
Определение геометрической прогрессии помогает нам анализировать и находить суммы членов прогрессии, а также решать много других математических задач. Понимание особенностей этого типа последовательности позволяет нам использовать их в реальных ситуациях, например, в финансовых расчетах или при решении задач связанных с ростом и убыванием популяции.
Формула для нахождения суммы шести чисел геометрической прогрессии

Для нахождения суммы шести чисел в геометрической прогрессии применяется следующая формула:
| S6 = a1 * (1 - qn) / (1 - q) |
Где:
- S6 - сумма шести чисел геометрической прогрессии;
- a1 - первый член геометрической прогрессии;
- q - знаменатель прогрессии;
- n - количество членов прогрессии (в данном случае 6).
Подставив значения в формулу, можно получить сумму шести чисел геометрической прогрессии.
Например, если первый член геометрической прогрессии равен 2, знаменатель прогрессии равен 3 и количество членов равно 6, то:
| S6 = 2 * (1 - 36) / (1 - 3) = 2 * (-728) / (-2) = 728 |
Сумма шести чисел геометрической прогрессии равна 728.
Полезные советы для упрощения вычислений

Вычисление суммы шести чисел геометрической прогрессии может показаться сложной задачей. Однако, с помощью некоторых полезных советов, этот процесс можно значительно упростить.
1. Найдите первый элемент, последний элемент и число членов прогрессии. Убедитесь, что вы правильно определили значения всех этих параметров.
2. Обратите внимание на разность (уже найденного) первого и последнего элементов. Если разность меньше 1, значит, прогрессия убывающая, а если больше 1 - возрастающая.
3. Используйте формулу для суммы геометрической прогрессии:
| Тип прогрессии | Формула |
|---|---|
| Возрастающая | S = a * (r^n - 1) / (r - 1) |
| Убывающая | S = a * (1 - r^n) / (1 - r) |
Где S - сумма прогрессии, a - первый элемент, r - знаменатель (отношение между соседними элементами), n - количество элементов в прогрессии.
4. Замените значения в формуле на найденные параметры и выполните вычисления.
5. Убедитесь, что ваш ответ имеет правильный формат и точность.
Следуя этим простым советам, вы сможете легко и точно найти сумму шести чисел геометрической прогрессии. И не забывайте проверять свои вычисления!
Пример 1: нахождение суммы шести чисел геометрической прогрессии с известными значениями

Для нахождения суммы шести чисел геометрической прогрессии, воспользуемся формулой:
Sn = a1(1 - qn) / (1 - q)
Где:
- Sn - сумма первых n членов прогрессии
- a1 - первый член прогрессии
- q - знаменатель прогрессии
- n - количество членов прогрессии
Предположим, что у нас есть геометрическая прогрессия с первым членом a1 = 2 и знаменателем q = 3. Мы хотим найти сумму первых шести членов этой прогрессии.
Подставим значения в формулу:
S6 = 2(1 - 36) / (1 - 3)
Вычислим значение в скобках:
S6 = 2(1 - 729) / (1 - 3)
Упростим выражение:
S6 = 2(-728) / (-2)
S6 = 728 / 2
S6 = 364
Таким образом, сумма первых шести чисел геометрической прогрессии с первым членом 2 и знаменателем 3 равна 364.
Пример 2: нахождение суммы шести чисел геометрической прогрессии со сложными значениями

Допустим, нам нужно найти сумму шести чисел геометрической прогрессии, но значения этих чисел выглядят сложными или необычными.
Предположим, что у нас есть геометрическая прогрессия, в которой первый элемент равен 1, а знаменатель равен равен 2. Как мы можем найти сумму шести элементов этой прогрессии, если нам необходимо использовать сложные значения вместо простых чисел?
В таком случае мы можем использовать формулу для суммы геометрической прогрессии:
Sn = a * (qn - 1) / (q - 1)
Где:
- Sn - сумма первых n элементов прогрессии
- a - первый элемент прогрессии
- q - знаменатель прогрессии
Нам нужно найти сумму шести элементов геометрической прогрессии, поэтому n = 6. Первый элемент равен 1, а знаменатель равен 2. Подставим эти значения в формулу:
S6 = 1 * (26 - 1) / (2 - 1) = 1 * (64 - 1) / 1 = 63
Таким образом, сумма шести элементов геометрической прогрессии со значениями 1 и 2 равна 63.