Треугольник является одной из основных геометрических фигур, изучаемых в 8 классе. Знание суммы углов треугольника является необходимым для решения различных задач и уравнений. Углы в треугольнике имеют важное значение, так как определяют его форму и свойства. Поэтому понимание, как найти сумму углов треугольника, является важным навыком для учеников 8 класса.
Сумма углов треугольника равна 180 градусам. Это единственное свойство углов в треугольнике, которое помогает нам решать различные задачи и находить значения неизвестных углов. Давайте рассмотрим подробнее, как находить сумму углов треугольника.
Для этого можно использовать несколько способов. Один из них - использование известных свойств геометрических фигур. Например, мы можем разбить треугольник на два прямоугольных треугольника. Так как сумма углов в прямоугольном треугольнике равна 90 градусам, мы можем выразить сумму углов в треугольнике через сумму углов в прямоугольных треугольниках.
Как найти сумму углов треугольника
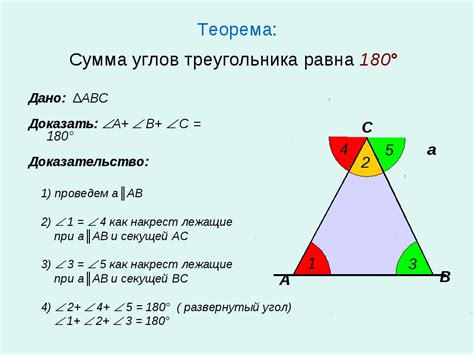
Сумма углов треугольника всегда равна 180 градусам. Это основное свойство треугольника и оно верно для всех треугольников независимо от их типа (равносторонний, равнобедренный, разносторонний).
Для нахождения суммы углов треугольника можно использовать несколько подходов:
1. Используя известные углы. Если известны два угла треугольника, то третий угол можно найти, вычтя сумму известных углов из 180 градусов. Например, если известны углы А (60 градусов) и В (40 градусов), то третий угол С можно найти следующим образом: С = 180 - (А + В) = 180 - (60 + 40) = 80 градусов.
2. Используя свойства треугольника. Если известны длины сторон треугольника, то можно воспользоваться теоремой косинусов для нахождения углов. Например, если известны длины сторон АВ (5 см), ВС (4 см) и СА (3 см), то угол А можно найти по формуле: А = arccos((ВС^2 + СА^2 - АВ^2) / (2 * ВС * СА)) = arccos((4^2 + 3^2 - 5^2) / (2 * 4 * 3)) ≈ 36,87 градусов. Аналогично можно найти остальные углы.
3. Используя свойства равностороннего треугольника. В равностороннем треугольнике все углы равны между собой и равны 60 градусам. Следовательно, сумма углов равностороннего треугольника тоже равна 180 градусам.
4. Используя таблицу углов. В крайнем случае, если необходима быстрая проверка, можно воспользоваться таблицей углов треугольников. В таблице указаны стандартные значения углов для разных типов треугольников. Например, для равнобедренного треугольника углы между основанием и равными сторонами равны 180 градусов минус двойное значение угла основания.
| Тип треугольника | Условия | Сумма углов |
|---|---|---|
| Равносторонний | Все стороны равны между собой | 180 градусов |
| Равнобедренный | Две стороны равны между собой | 180 градусов минус двойное значение угла основания |
| Прямоугольный | Один угол равен 90 градусам | 180 градусов |
| Разносторонний | Все стороны и углы различны | 180 градусов |
Независимо от используемого подхода или метода, сумма углов треугольника всегда будет равна 180 градусам, что позволяет проводить различные вычисления и анализ свойств треугольников.
Углы треугольника и их свойства
В треугольнике есть три угла, которые суммарно равны 180 градусам. Это важное свойство треугольника, которое всегда остается верным, независимо от его формы и размеров.
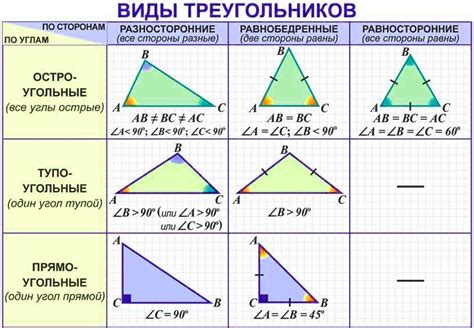
Рассмотрим основные типы углов треугольника:
| Тип угла | Описание |
|---|---|
| Острый угол | Угол, меньший 90 градусов. |
| Прямой угол | Угол, равный 90 градусам. Он образуется между двумя перпендикулярными сторонами треугольника. |
| Тупой угол | Угол, больший 90 градусов, но меньший 180 градусов. |
| Равнобедренный угол | Угол, который образуется между двумя равными сторонами треугольника. |
| Равносторонний угол | Угол, все стороны треугольника которого равны. |
Зная свойства углов треугольника, мы можем решать различные задачи, например, вычислять недостающие углы или стороны треугольника, проверять, является ли треугольник прямоугольным и многое другое.
Сумма углов треугольника и ее особенности

Сумма углов треугольника обусловлена геометрической особенностью, именуемой "угловая сумма треугольника". Угол в треугольнике представляет собой раскрытие одной из его сторон относительно другой. Каждая сторона имеет свой угол, а суммарное раскрытие всех сторон всегда равно 360 градусам. В треугольнике имеется три стороны, а значит, раскрытие всех трех сторон равно 180 + 180 + 180 = 540 градусам. Однако, каждая сторона влияет на замыкание углов других сторон, что приводит к сумме углов, равной 180 градусам.
Сумма углов треугольника является основой для различных геометрических вычислений и задач. Зная значение двух углов, можно легко определить третий. Например, если один угол треугольника равен 60 градусам, а второй – 50 градусам, то третий угол равен 180 - 60 - 50 = 70 градусам.
Сумма углов треугольника также позволяет определить, является ли фигура треугольником или нет. Если сумма углов трех линий в фигуре составляет 180 градусов, то это треугольник. Если сумма больше или меньше 180 градусов, то это уже не треугольник, а какая-то другая фигура.
Изучение суммы углов треугольника является важным элементом геометрии, "открывающим" школьникам много новых знаний и прикладных навыков. Понимание данного принципа помогает решать задачи по геометрии и строить корректные графические представления треугольников.
Формула для вычисления суммы углов треугольника

Сумма углов в любом треугольнике всегда равна 180 градусам.
Для вычисления суммы углов треугольника можно использовать следующую формулу:
Сумма углов треугольника = Угол 1 + Угол 2 + Угол 3
Где Угол 1, Угол 2 и Угол 3 - углы, составляющие треугольник.
Например, если у нас есть треугольник с углами 60°, 60° и 60°, то сумма этих углов будет равна:
Сумма углов треугольника = 60° + 60° + 60° = 180°
Таким образом, сумма углов треугольника всегда будет равна 180°, независимо от формы или размеров треугольника.
Примеры решения задач на вычисление суммы углов треугольника:

Пример 1:
Дан треугольник ABC, в котором угол B равен 45°, а угол C равен 60°. Найдем сумму всех углов данного треугольника.
Известно, что сумма углов треугольника равна 180°. Поэтому, чтобы найти угол A, необходимо вычислить разницу между 180° и суммой углов B и C.
A + B + C = 180°
A + 45° + 60° = 180°
A = 180° - 45° - 60° = 75°
Таким образом, сумма всех углов треугольника ABC равна 75° + 45° + 60° = 180°.
Пример 2:
Дан треугольник PQR, в котором угол Q равен 90°, а угол R равен 30°. Найдем сумму всех углов данного треугольника.
Известно, что сумма углов треугольника равна 180°. Поэтому, чтобы найти угол P, необходимо вычислить разницу между 180° и суммой углов Q и R.
P + Q + R = 180°
P + 90° + 30° = 180°
P = 180° - 90° - 30° = 60°
Таким образом, сумма всех углов треугольника PQR равна 60° + 90° + 30° = 180°.
Пример 3:
Дан треугольник XYZ, в котором угол X равен 60°, а угол Z равен 75°. Найдем сумму всех углов данного треугольника.
Известно, что сумма углов треугольника равна 180°. Поэтому, чтобы найти угол Y, необходимо вычислить разницу между 180° и суммой углов X и Z.
X + Y + Z = 180°
60° + Y + 75° = 180°
Y = 180° - 60° - 75° = 45°
Таким образом, сумма всех углов треугольника XYZ равна 60° + 45° + 75° = 180°.
Задачи с самостоятельным решением на вычисление суммы углов треугольника

Решение задач на вычисление суммы углов треугольника включает в себя применение базовых знаний о геометрии и свойствах треугольников. Эти задачи позволяют закрепить полученные знания, развить логическое мышление и умение применять формулы.
Вот несколько простых задач, которые вы можете решить самостоятельно:
- Найдите сумму углов треугольника, если один из углов равен 60°, а два других угла равны между собой.
- У треугольника один угол равен 90°, а два других угла равны между собой. Найдите сумму этих углов.
- В треугольнике один угол равен 30°, а два других угла равны между собой. Найдите сумму этих углов.
Чтобы решить эти задачи, вы можете использовать следующую формулу: сумма углов треугольника равна 180°. Таким образом, для первой задачи с углом 60° вы можете использовать следующее уравнение: 60° + 2x = 180°, где x - неизвестный угол треугольника. Решите это уравнение, чтобы найти значение x и далее вычислить сумму всех углов треугольника.
После того, как вы решили эти простые задачи, попробуйте решить более сложные задачи, которые могут включать углы разного размера и использование свойств треугольников, таких как углы, смежные к сторонам треугольника.
Решая задачи на вычисление суммы углов треугольника, вы разовьете свои навыки в геометрии и логическом мышлении, а также укрепите свои знания о треугольниках.
Треугольники: особенности и свойства
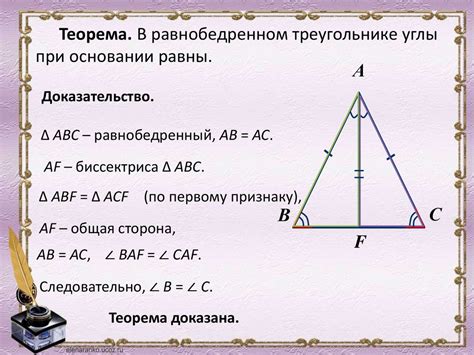
Типы треугольников
Существует несколько различных типов треугольников, которые можно классифицировать в зависимости от своих свойств:
- Равносторонний треугольник: все три стороны равны друг другу, а все три угла - по 60 градусов.
- Равнобедренный треугольник: две стороны равны, а два угла - равны.
- Прямоугольный треугольник: один из углов является прямым (равным 90 градусов).
- Остроугольный треугольник: все три угла острые (меньше 90 градусов).
- Тупоугольный треугольник: один из углов является тупым (больше 90 градусов).
Свойства треугольников
У треугольников также есть несколько важных свойств, которые помогают нам их изучать и решать задачи:
- Сумма углов треугольника: сумма всех трех углов всегда равна 180 градусам.
- Теорема Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
- Неравенство треугольника: сумма длин любых двух сторон треугольника всегда больше третьей стороны.
- Формулы для вычисления площади: существует несколько формул, позволяющих вычислить площадь треугольника в зависимости от известных данных.
Заключение