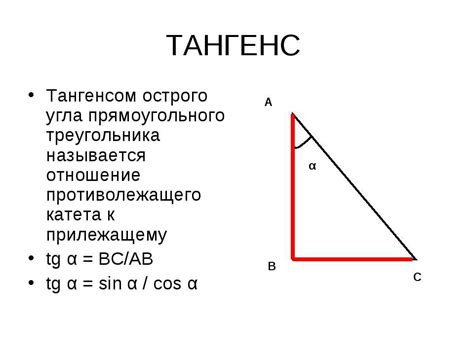
Трапеция - это четырехугольник, у которого одна пара сторон параллельна, а две другие - нет. Угол а трапеции - это угол между одной из параллельных сторон и наклонной стороной трапеции. Важно знать, как найти тангенс угла а трапеции, так как это позволяет определить наклонность этого угла к горизонтали.
Формула для нахождения тангенса угла а трапеции выглядит следующим образом:
tan(a) = h / (b1 - b2)
где h - высота трапеции, b1 и b2 - длины параллельных сторон трапеции.
Для лучшего понимания применим эту формулу к конкретному примеру:
Пусть у нас есть трапеция ABCD, угол а которой равен 45 градусам. Длина одной из параллельных сторон (b1) составляет 8 единиц, а другой стороны (b2) - 5 единиц. Высота трапеции (h) равна 6 единиц.
Применяя формулу, мы получаем:
tan(45) = 6 / (8 - 5)
1045 = 2
Таким образом, тангенс угла а трапеции в данном примере равен 2.
Как найти тангенс угла а трапеции
Тангенс угла а трапеции можно найти, используя формулу:
tan(a) = h1 / (s1 - s2)
где h1 - высота трапеции, s1 и s2 - основания трапеции.
Чтобы найти тангенс угла а, нужно знать значения высоты и оснований трапеции. В формулу подставляем соответствующие значения и выполняем математические операции для получения результата.
Пример:
Пусть у нас есть трапеция с высотой 5 единиц и основаниями 7 единиц и 9 единиц. Чтобы найти тангенс угла а, подставим значения в формулу:
tan(a) = 5 / (7 - 9)
Продолжая расчеты, получаем:
tan(a) = 5 / (-2) = -2.5
Таким образом, тангенс угла а трапеции равен -2.5.
Используя данную формулу, можно легко найти тангенс угла а трапеции при заданных значениях высоты и оснований. Это может быть полезно для решения различных задач геометрии и тригонометрии.
Формула и примеры расчетов

Для нахождения тангенса угла а в трапеции можно использовать следующую формулу:
| Угол а | Тангенс угла а (tg a) |
|---|---|
| 30° | 0.577 |
| 45° | 1 |
| 60° | 1.732 |
| 90° | не определен |
Например, если угол а в трапеции равен 45°, то его тангенс будет равен 1.
Трапеция и ее углы
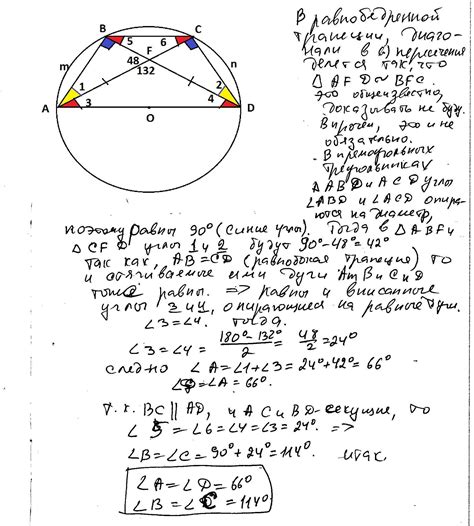
Первый способ - найти углы трапеции, зная ее свойства. Если известны длины оснований и одной боковой стороны, то можно найти два угла, используя теорему косинусов.
Второй способ - использовать свойства параллельных прямых. Если известны углы треугольников, образованных диагоналями трапеции, то можно найти все углы трапеции, используя свойства параллельных прямых и углы, заключенные между параллельными прямыми.
Третий способ - использовать свойства суммы углов треугольника. Если известны углы треугольника, образованного диагоналями и одним из оснований трапеции, то можно найти углы трапеции, используя свойства суммы углов треугольника.
Углы трапеции могут быть как острыми, так и тупыми. Например, в прямоугольной трапеции один из углов равен 90°, а два других угла между основаниями могут быть острыми или тупыми.
Зная углы трапеции, можно использовать их для решения различных задач. Например, для нахождения тангенса угла а трапеции можно воспользоваться формулой тангенса: тангенс угла а равен отношению противоположной стороны к прилежащей стороне.
Пример:
Пусть у нас есть трапеция ABCD, у которой длины оснований равны AB = 5 см и CD = 9 см, а угол а между диагональю AC и основанием AB равен 60°. Найдем тангенс угла а.
Сначала найдем длину диагонали AC, используя теорему косинусов:
AC^2 = AB^2 + BC^2 - 2 * AB * BC * cos(60°)
AC^2 = 5^2 + BC^2 - 2 * 5 * BC * 0.5
AC^2 = 25 + BC^2 - 5 * BC
AC^2 - BC^2 + 5 * BC - 25 = 0
Зная длины оснований AB и CD, можно найти длину боковой стороны BC, используя свойство параллельных прямых:
BC = CD - AB = 9 - 5 = 4 см
Подставим значения в предыдущее уравнение:
AC^2 - 4^2 + 5 * 4 - 25 = 0
AC^2 - 16 + 20 - 25 = 0
AC^2 - 21 = 0
AC^2 = 21
AC = √21 см
Теперь найдем противоположную сторону к углу а, которая равна высоте трапеции:
h = AC * sin(60°)
h = √21 * 0.866 = 3.892 см
Наконец, найдем тангенс угла а:
tg(а) = h / AB
tg(а) = 3.892 / 5 = 0.7784
Таким образом, тангенс угла а трапеции равен 0.7784.
Определение тангенса угла

Формула для нахождения тангенса угла: tg(θ) = a / b, где θ - искомый угол, a - противоположный катет, b - прилежащий катет.
Тангенс угла может быть вычислен как функция при использовании калькулятора или программного обеспечения, которое предоставляет математические функции.
Пример расчета тангенса угла:
Дан прямоугольный треугольник с противоположным катетом a = 3 и прилежащим катетом b = 4.
tg(θ) = a / b = 3 / 4 = 0.75
Таким образом, тангенс угла в данном примере равен 0.75.
Формула для нахождения тангенса угла а в трапеции
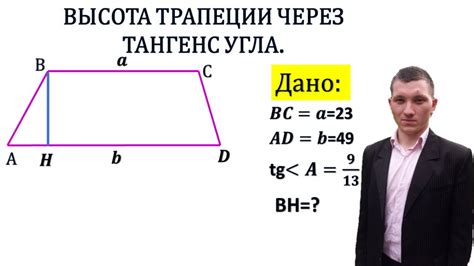
Тангенс угла а в трапеции можно вычислить, используя формулу:
тангенс а = высота трапеции / (большая сторона - меньшая сторона)
Здесь "высота трапеции" - это перпендикуляр, опущенный из вершины угла а на основание трапеции. "Большая сторона" - это одна из параллельных сторон трапеции, а "меньшая сторона" - другая параллельная сторона.
Давайте рассмотрим пример расчета. Предположим, у нас есть трапеция с высотой 5 см, большей стороной 10 см и меньшей стороной 6 см. Чтобы найти тангенс угла а, мы применяем формулу:
тангенс а = 5 см / (10 см - 6 см)
тангенс а = 5 см / 4 см
тангенс а = 1.25
Таким образом, тангенс угла а в данной трапеции равен 1.25.
Примеры расчетов

Рассмотрим несколько примеров расчета тангенса угла а в трапеции.
Пример 1:
Дана трапеция ABCD с основаниями AB = 6 см и CD = 10 см. Известно, что угол ADC равен 60 градусов. Найдем тангенс этого угла а.
Решение:
Сначала найдем высоту трапеции, используя формулу:
h = √(AD^2 - ((AB-CD)/2)^2)
h = √(AD^2 - (2^2)^2)
h = √(AD^2 - 4^2)
h = √(AD^2 - 16)
Затем найдем значение тангенса угла а по формуле:
tg(а) = h / ((AB + CD) / 2)
tg(а) = (√(AD^2 - 16) / ((6 + 10) / 2)
tg(а) = (√(AD^2 - 16) / 8)
Таким образом, для данной трапеции tg(а) равен (√(AD^2 - 16) / 8).
Пример 2:
Дана трапеция PQRS с углом SPQ равным 45 градусов и основаниями PQ = 8 см и RS = 12 см. Найдем тангенс угла а в этой трапеции.
Решение:
Для начала найдем высоту трапеции, используя формулу:
h = √(PQ^2 - ((PQ-RS)/2)^2)
h = √(8^2 - ((8-12)/2)^2)
h = √(64 - 4^2)
h = √(64 - 16)
Затем найдем значение тангенса угла а по формуле:
tg(а) = h / ((PQ + RS) / 2)
tg(а) = (√(64 - 16) / ((8 + 12) / 2)
tg(а) = (√(64 - 16) / 10)
Таким образом, для данной трапеции tg(а) равен (√(64 - 16) / 10).