Тангенс угла – это одна из шести основных тригонометрических функций, которая широко применяется в различных областях науки, инженерии и математике. Нахождение тангенса угла может быть полезно для решения задач в геометрии, физике, астрономии и других дисциплинах.
Тангенс угла определяется как отношение противоположной стороны треугольника к прилежащей стороне. Другими словами, тангенс угла равен отношению синуса угла к косинусу угла. Математически это записывается формулой: tg(α) = sin(α) / cos(α).
Существует несколько способов нахождения тангенса угла. Один из самых простых способов – использование таблицы тангенсов, в которой указаны значения тангенса для различных углов. Второй способ – использование калькулятора, где есть функция нахождения тангенса. Наконец, можно применить формулу, зная значения синуса и косинуса угла.
Зачем нужен тангенс угла?

Тангенс широко применяется в различных областях, включая математику, физику, инженерию и астрономию. Например, в физике тангенс используется для расчета силы трения, а в астрономии - для определения расстояния до звезд.
Тангенс также полезен при решении задач геометрии и тригонометрии, а также при построении графиков функций. Он может помочь в определении углов наклона, углов поворота и других геометрических параметров.
Изучение тангенса угла является важной частью математического образования и может быть полезно в реальной жизни, чтобы упростить и ускорить вычисления и решение задач.
Как найти тангенс угла вручную?

Если у вас есть треугольник, в котором известны длины сторон, то тангенс угла можно найти по формуле:
тангенс угла = противоположная сторона / прилежащая сторона.
Например, если противоположная сторона равна 5, а прилежащая сторона равна 3, то тангенс угла будет равен 5/3 или примерно 1.67.
Если у вас нет треугольника, можно воспользоваться таблицами значений тангенса. В этом случае нужно найти значение тангенса для данного угла в таблице и использовать его.
Например, если вам нужно найти тангенс угла в 45 градусов, то в таблице вы найдете, что тангенс 45 градусов равен 1.
Иногда может потребоваться найти тангенс угла с помощью математических формул, например, если у вас есть значение синуса и косинуса угла. В этом случае можно воспользоваться формулой:
тангенс угла = синус угла / косинус угла.
Например, если синус угла равен 0.5, а косинус угла равен 0.866, то тангенс угла будет равен 0.5 / 0.866 или примерно 0.577.
Формула нахождения тангенса угла
Математическая формула для нахождения тангенса угла:
тангенс (tg) угла = противоположная сторона / прилежащая сторона
Тангенс угла можно вычислить, используя значения сторон треугольника или известные значения углов. Например, если известны значения сторон прямоугольного треугольника, можно использовать соответствующую сторону и противоположующую сторону, чтобы вычислить тангенс угла.
Помните, что при нахождении тангенса угла важно учитывать единицы измерения угла: градусы, радианы или грады. Не забывайте указывать единицы измерения в вашем ответе.
Примеры расчета тангенса угла
Вот несколько примеров, которые помогут вам понять, как рассчитать тангенс угла:
- Пример 1: Рассчитаем тангенс угла 45°. Подставим значение угла в формулу тангенса:
тангенс 45° = sin 45° / cos 45°
Поскольку значение синуса и косинуса 45° равны 1 / √2, соответственно, мы можем записать:
тангенс 45° = (1 / √2) / (1 / √2)
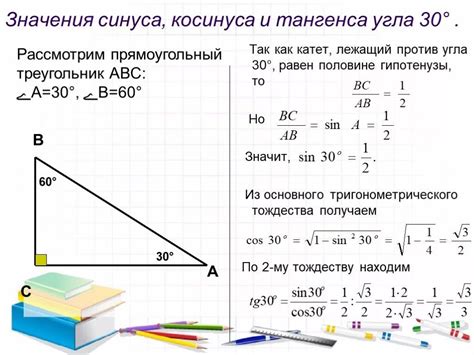
После сокращения дроби мы получаем тангенс 45° = 1. - Пример 2: Рассчитаем тангенс угла 30°. Запишем угол в радианах, так как большинство функций тригонометрии принимают радианы:
тангенс 30° = sin (30° * π / 180) / cos (30° * π / 180)
Значение синуса и косинуса 30° в радианах равны 1 / 2 и √3 / 2, соответственно, поэтому мы можем записать:
тангенс 30° = (1 / 2) / (√3 / 2) = 1 / √3 - Пример 3: Рассчитаем тангенс угла 60°:
тангенс 60° = sin (60° * π / 180) / cos (60° * π / 180)
Значение синуса и косинуса 60° в радианах равны √3 / 2 и 1 / 2, соответственно, поэтому мы можем записать:
тангенс 60° = (√3 / 2) / (1 / 2) = √3
Это лишь несколько примеров расчета тангенса угла. Вы можете использовать формулу тангенса и данные таблицы синусов и косинусов, чтобы рассчитать тангенс любого угла. Помните, что значение тангенса может быть отрицательным, положительным или нулевым, в зависимости от значения угла.
Как найти тангенс угла с использованием калькулятора?

Для нахождения тангенса угла с использованием калькулятора, вам потребуется выполнить следующие шаги:
- Включите калькулятор: Убедитесь, что ваш калькулятор включен и готов к работе.
- Выберите режим работы: Найдите на калькуляторе кнопку или переключатель, который позволяет переключаться между различными режимами работы. В большинстве случаев это будет кнопка "MODE" или что-то похожее. Выберите режим тригонометрии.
- Ввод угла: Введите значение угла, для которого нужно найти тангенс. Убедитесь в правильности ввода, чтобы получить точный результат.
- Найдите тангенс: Найдите на калькуляторе кнопку, помеченную как "TAN" или "tg". Нажмите эту кнопку, чтобы получить значение тангенса угла.
- Оцените результат: Просмотрите полученное значение тангенса и удостоверьтесь, что оно соответствует вашим ожиданиям.
Использование калькулятора для нахождения тангенса угла является быстрым и удобным способом получить результат. Помните, что значение тангенса может быть отрицательным или бесконечным в зависимости от угла и его положения на окружности.
Обратите внимание: При использовании калькулятора для нахождения тангенса угла, применяйте осторожность и проверяйте вводимые значения, чтобы избежать ошибок.