Равнобедренный треугольник - это треугольник, у которого две стороны равны. Изучение равнобедренных треугольников позволяет нам легко находить все углы и стороны треугольника. Один из способов решения задачи, связанных с равнобедренным треугольником, состоит в определении тангенса угла.
Тангенс угла в равнобедренном треугольнике можно найти, используя простую формулу. Для этого нужно знать значение угла и длину одной из равных сторон. Формула выглядит следующим образом: тангенс угла равен отношению противолежащей стороны к прилежащей стороне.
Формула нахождения тангенса угла в равнобедренном треугольнике выглядит так:
тангенс угла = противолежащая сторона / прилежащая сторона
Выражение "противолежащая сторона" обозначает сторону, которая лежит напротив заданного угла в треугольнике, а "прилежащая сторона" - сторону, которая примыкает к этому углу.
После подстановки в формулу известной длины сторон, мы можем рассчитать тангенс угла в равнобедренном треугольнике. Этот результат может быть полезным, когда требуется определить угол по его тангенсу или наоборот, найти тангенс угла.
<>Равнобедренный треугольник: тангенс угла и его расчет
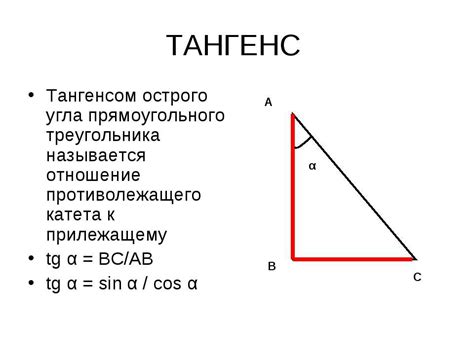
Один из важных параметров равнобедренного треугольника – это тангенс угла, определяемый отношением противолежащей стороны к прилежащей стороне. Для нахождения тангенса угла в равнобедренном треугольнике существуют специальные формулы.
Формула для расчета тангенса угла в равнобедренном треугольнике выглядит следующим образом:
tg(α) = (a / 2) / h
Где α – угол между базой и боковой стороной равнобедренного треугольника, a – длина базы, h – высота проведенная из вершины до базы.
Чтобы найти тангенс угла в равнобедренном треугольнике, нужно знать значения стороны базы и высоты.
Пример расчета тангенса угла в равнобедренном треугольнике:
Предположим, у нас есть равнобедренный треугольник ABC, где AC – база, h – высота, и требуется найти tg(α).
Если значение базы AC = 8 см, а высоты h = 4 см, то подставив в формулу получим:
tg(α) = (8 / 2) / 4
tg(α) = 4 / 4 = 1
Таким образом, в данном случае тангенс угла α равен 1.
Теперь вы знаете, как найти тангенс угла в равнобедренном треугольнике с помощью соответствующей формулы и проведения расчетов.
Определение равнобедренного треугольника
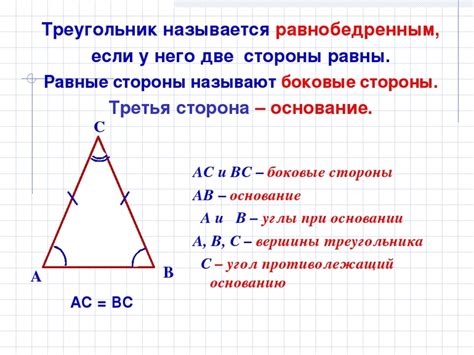
Особенностью равнобедренного треугольника является то, что у него два угла также имеют одинаковую величину, и они противолежат равным сторонам. Такие треугольники могут быть как прямоугольными, так и непрямоугольными.
Применяется понятие равнобедренного треугольника в различных областях, например, в геометрии, в физике и в технике. Уравнение равнобедренного треугольника можно решить с использованием математических формул и правил.
Формула нахождения тангенса угла в равнобедренном треугольнике

Формула выглядит так:
| Формула | Расчет |
|---|---|
| tg ≈ | длина противолежащего катета / длина прилежащего катета |
Для нахождения тангенса угла в равнобедренном треугольнике нужно знать длину противолежащего катета и длину прилежащего катета. Длина противолежащего катета - это длина основания треугольника, а длина прилежащего катета - это длина одного из боковых сторон.
Применяя данную формулу, можно вычислить тангенс угла в равнобедренном треугольнике, что может быть полезно для решения различных геометрических задач и вычислений.
Пример расчета тангенса угла в равнобедренном треугольнике

Рассмотрим пример расчета тангенса угла в равнобедренном треугольнике. Пусть у нас есть треугольник ABC, в котором угол A равен 45 градусов, а сторона AB равна 10 единиц. Нам нужно найти тангенс угла A.
Для начала, воспользуемся формулой для тангенса угла:
tan(A) = (противолежащая сторона) / (прилежащая сторона)
В нашем случае, противолежащая сторона угла A - это сторона AC, а прилежащая сторона - сторона AB.
Таким образом, у нас есть:
tan(A) = AC / AB
Подставим известные значения:
tan(45) = AC / 10
Далее, рассчитаем значение AC, используя свойство равнобедренного треугольника. В равнобедренном треугольнике две стороны, прилегающие к углу A, равны между собой.
Таким образом, сторона AC равна стороне AB, то есть 10 единиц.
Подставим значение AC в нашу формулу:
tan(45) = 10 / 10
Упростим выражение:
tan(45) = 1
Итак, тангенс угла A в равнобедренном треугольнике с углом 45 градусов равен 1.
Применение тангенса угла в равнобедренном треугольнике

Тангенс угла в равнобедренном треугольнике находит свое применение при решении различных задач, связанных с геометрией и тригонометрией.
Одним из основных применений тангенса является нахождение отношения высоты треугольника к основанию. В равнобедренном треугольнике, высота, опущенная из вершины до основания, является медианой, биссектрисой и высотой одновременно. Таким образом, найти отношение высоты к основанию можно, используя тангенс угла приложения высоты.
Для расчета отношения высоты к основанию можно воспользоваться следующей формулой:
h = b * tan(α/2)
где:
- h - высота треугольника;
- b - длина основания треугольника;
- α - мера угла приложения высоты.
Таким образом, зная длину основания треугольника и меру угла приложения высоты, можно легко найти высоту треугольника, используя тангенс.
Тангенс угла в равнобедренном треугольнике можно вычислить с помощью простой формулы. Для этого нужно знать значение угла и длину любой из его сторон. Формула для вычисления тангенса угла в равнобедренном треугольнике выглядит следующим образом:
tg(α) = a/((b/2)×√(4×a²-(b²/2)))
где α - угол, a - длина основания, b - длина боковой стороны треугольника.
Таким образом, чтобы найти тангенс угла в равнобедренном треугольнике, нужно подставить известные значения в данную формулу и выполнить вычисления.
Определяя тангенс угла, мы можем получить полезную информацию о свойствах и геометрии равнобедренного треугольника и использовать его в дальнейших вычислениях и решении различных задач.