Треугольник - это геометрическая фигура, состоящая из трех сторон и трех углов. Всякий треугольник имеет свои уникальные свойства и характеристики, которые можно рассчитать с помощью различных математических формул и правил. Одними из таких характеристик являются углы треугольника.
Тангенс угла - это соотношение между противоположной и прилежащей к ней сторонами прямоугольного треугольника. Это важное понятие для решения различных геометрических задач и вычислений. Особый интерес представляет нахождение тангенса угла в треугольнике центр.
Треугольник центр - это треугольник с высотами, проведенными из его вершин к противоположным сторонам. В таком треугольнике центральный угол с радиусом, проведенным к центру вписанной окружности, является исходным углом. Найти тангенс такого угла можно, разделив противоположную катету на прилежащий катет.
Определение треугольника центр
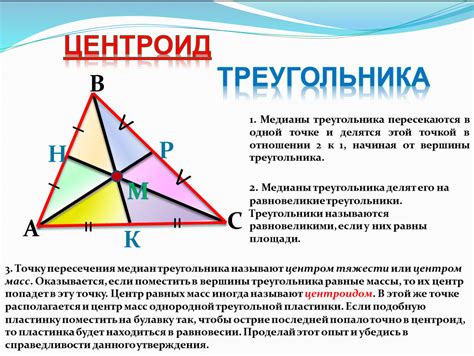
Треугольник центр является важным понятием в геометрии, так как демонстрирует некоторые интересные свойства и связи с остальными элементами треугольника. Например, медианы, проходящие через треугольник центр, делятся им в отношении 2:1. То есть, расстояние от вершины треугольника до треугольника центр в два раза больше, чем расстояние от треугольника центр до противоположной стороны.
Точное определение треугольника центр может быть получено с помощью математических вычислений на основе координат вершин треугольника. Однако, существуют и альтернативные способы нахождения треугольника центр, которые не требуют сложных вычислений.
| Тип треугольника | Координаты треугольника центр |
|---|---|
| Равносторонний треугольник | Точка с одинаковыми координатами вершин треугольника |
| Равнобедренный треугольник | Точка на симметрии оси треугольника, проходящей через биссектрису угла и основание |
| Прямоугольный треугольник | Точка, являющаяся серединой гипотенузы |
| Произвольный треугольник | Точка, найденная путем пересечения трех медиан треугольника |
Треугольник центр играет важную роль в свойствах и приложениях треугольников, поэтому его определение и изучение является важным этапом для понимания геометрии треугольников.
Что такое треугольник центр

Один из самых важных центров треугольника – центр описанной окружности. Он определяется как точка пересечения всех перпендикуляров, проведенных из середин сторон треугольника к противоположным углам.
Другой важный центр треугольника – центр вписанной окружности. Он определяется как точка пересечения биссектрис треугольника.
Центр тяжести треугольника – это точка пересечения медиан треугольника, проведенных из вершин к серединам противоположных сторон.
Каждый из центров имеет свои уникальные свойства и применяется для решения различных задач в геометрии. Понимание и использование центров треугольника является важным для изучения геометрии и решения разнообразных математических задач.
Важно: знание треугольника центра может быть полезно для решения задач, связанных с поиском тангенса угла в треугольнике, так как свойства данных центров могут быть использованы для определения отношений между сторонами и углами треугольника.
Формула для нахождения тангенса угла в треугольнике центр

В треугольнике центр тангенс угла может быть найден с помощью следующей формулы:
- Найдите величину противоположной стороны треугольника, применяя известную формулу синуса: синус угла равен отношению длины противоположной стороны к длине гипотенузы.
- Найдите величину прилежащей стороны треугольника, применяя известную формулу косинуса: косинус угла равен отношению длины прилежащей стороны к длине гипотенузы.
- Разделите значение противоположной стороны на значение прилежащей стороны, чтобы найти тангенс угла.
Формула для нахождения тангенса угла в треугольнике центр может быть полезна при решении различных геометрических задач, связанных с треугольниками и их углами.
Общая формула

Для нахождения тангенса угла в треугольнике центр существует общая формула:
tg(A) = a / b
где tg(A) - тангенс угла A,
a - противолежащая сторона угла A,
b - прилежащая сторона угла A.
Эта формула позволяет найти значение тангенса угла в треугольнике центр и используется в геометрии и тригонометрии для решения различных задач и вычислений.
Пример:
В треугольнике ABC с углом A в радианах равным 1.2 и противолежащей стороной a равной 5, и прилежащей стороной b равной 3, можно найти тангенс угла A следующим образом:
tg(A) = a / b = 5 / 3 = 1.6667
Таким образом, тангенс угла A в данном треугольнике равен 1.6667.
Пример нахождения тангенса угла в треугольнике центр

Для того чтобы найти тангенс угла в треугольнике центр, необходимо знать значение этого угла и противолежащую сторону.
- Предположим, у нас есть треугольник центр ABC, где угол A равен 45 градусов, а сторона BC, противолежащая этому углу, равна 7 сантиметров.
- Далее, мы используем определение тангенса: тангенс угла равен отношению противолежащей стороны к прилежащей.
- В данном случае, для нахождения тангенса угла A мы делим длину стороны BC на длину стороны AC.
- Таким образом, тангенс угла A равен 7/AC.
Таким образом, при наших исходных данных, тангенс угла A в треугольнике центр ABC равен 7/AC. Для того чтобы найти значение тангенса угла A, необходимо знать длину стороны AC.
Конкретный пример
Рассмотрим пример вычисления тангенса угла в треугольнике центр с заданными значениями сторон и высоты.
Дано:
| Сторона a | Сторона b | Сторона c | Высота h |
|---|---|---|---|
| 5 см | 4 см | 6 см | 3 см |
Шаги для нахождения тангенса угла:
- Найдите полупериметр треугольника: p = (a + b + c) / 2
- Вычислите площадь треугольника: S = √(p * (p - a) * (p - b) * (p - c))
- Вычислите значение синуса угла: sin α = (2 * S) / (a * h)
- Вычислите значение косинуса угла: cos α = (2 * S) / (b * h)
- Вычислите значение тангенса угла: tan α = sin α / cos α
Подставляя заданные значения:
- p = (5 + 4 + 6) / 2 = 7.5
- S = √(7.5 * (7.5 - 5) * (7.5 - 4) * (7.5 - 6)) ≈ 9.92156759
- sin α = (2 * 9.92156759) / (5 * 3) ≈ 0.662771854
- cos α = (2 * 9.92156759) / (4 * 3) ≈ 0.828464818
- tan α = sin α / cos α ≈ 0.799092008
Таким образом, тангенс угла α в треугольнике центр с данными значениями сторон и высоты равен примерно 0.799092008.