Тангенс - это одна из основных тригонометрических функций, которая широко используется в математике и физике. Нахождение тангенса в треугольнике является важной задачей для решения различных геометрических и физических задач.
Существуют различные методы и формулы, позволяющие найти тангенс в треугольнике. Один из самых простых способов - это использование соотношения между сторонами треугольника и его углами. В прямоугольном треугольнике, например, тангенс угла можно найти как отношение противоположной стороны к прилежащей стороне.
Если треугольник не является прямоугольным, то можно использовать формулу для нахождения тангенса угла по заданным длинам сторон треугольника. Для этого можно воспользоваться формулой тангенса в общем виде: тангенс угла равен отношению противоположной стороны к прилежащей стороне. Для нахождения значения тангенса можно использовать встроенные функции калькулятора или специализированные программы и сайты.
Найти тангенс в треугольнике можно также с помощью таблицы тангенсов, в которой приведены значения тангенсов для различных углов. Это может быть особенно полезно, если нет возможности использовать калькулятор или компьютер. С помощью таблицы можно найти соответствующий угол и его тангенс, и затем использовать эти значения в дальнейших расчетах.
Тангенс в треугольнике: что это такое?
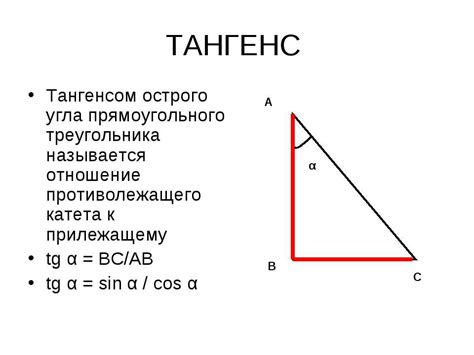
Точнее говоря, тангенс угла в треугольнике можно вычислить, поделив величину противоположной стороны к прилежащей стороне. Таким образом, тангенс выражается формулой:
тангенс угла (т) = противоположная сторона / прилежащая сторона
Тангенс представляет собой безразмерную величину и может принимать положительные и отрицательные значения, в зависимости от положения угла в треугольнике. Например, если угол противоположен стороне, то тангенс будет положительным. Если угол находится в другой части треугольника, то тангенс будет отрицательным.
Тангенс широко применяется в различных областях науки и техники, таких как физика, инженерия и геодезия. Он позволяет решать задачи, связанные с определением высот, дальности и направления, используя известные данные треугольника и тангенс угла.
Методы расчета тангенса в треугольнике
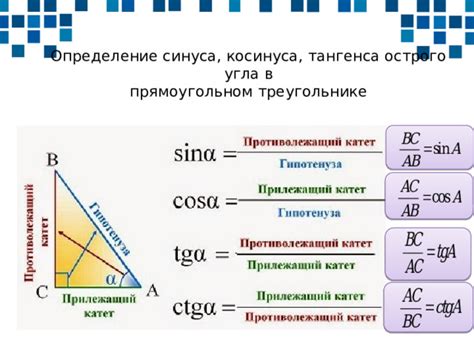
Существует несколько методов расчета тангенса в треугольнике, в зависимости от известных данных:
| Известные данные | Метод расчета тангенса |
|---|---|
| Длины сторон треугольника | Расчет тангенса через соотношение сторон |
| Значение угла треугольника | Расчет тангенса через тригонометрические функции |
| Координаты точек треугольника | Расчет тангенса через отношение координат |
Первый метод – расчет тангенса через соотношение сторон: тангенс угла треугольника равен отношению длины противолежащей стороны к длине прилежащей стороны. Формула для расчета тангенса в этом случае выглядит следующим образом:
тангенс угла = (длина противолежащей стороны) / (длина прилежащей стороны)
Второй метод – расчет тангенса через тригонометрические функции: для этого необходимо знать значение угла треугольника, который используется в качестве аргумента функции тангенс. Формула для расчета тангенса в этом случае выглядит следующим образом:
тангенс угла = tan(значение угла)
Третий метод – расчет тангенса через отношение координат: при заданных координатах точек треугольника можно использовать формулы для расчета сторон и затем расчитать тангенс угла с помощью первого метода.
Выбор метода расчета тангенса в треугольнике зависит от доступных данных и требований задачи. Важно помнить, что при расчете тангенса необходимо учитывать единицы измерения и приводить значения к одной системе, если это необходимо.
Формула для расчета тангенса треугольника
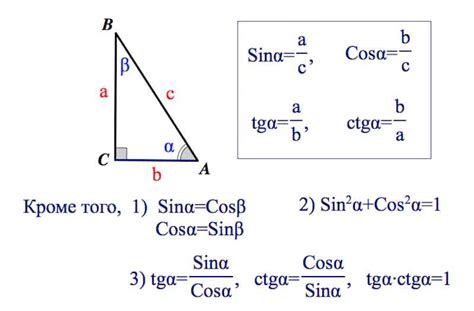
- Определите длины противоположной (a) и прилежащей (b) сторон треугольника.
- Рассчитайте тангенс треугольника, используя формулу:
- тангенс угла A = a / b
- тангенс угла B = b / a
- тангенс угла C = a / b
- Проверьте, что полученное значение тангенса соответствует ожидаемым результатам.
Расчет тангенса треугольника позволяет определить углы треугольника и использовать их для решения различных геометрических и физических задач, например, для определения высоты, длины сторон или определения направления движения.
Важно помнить, что для расчета тангенса треугольника необходимо знать длины сторон или хотя бы одну из них. Если известны только углы треугольника, необходимо использовать другие формулы, например, формулу синуса или косинуса.
Применение тангенса в практических задачах
Одной из наиболее распространенных практических задач, где применяется тангенс, является определение высоты объекта с помощью теодолита. Теодолит – это инструмент, который используется для измерения углов. С его помощью можно определить горизонтальный угол между наблюдателем, объектом и вертикальной осью теодолита. Затем, зная этот угол и расстояние до объекта, можно рассчитать высоту объекта с помощью тангенса.
Еще одной практической задачей, где применяется тангенс, является определение уклона склона. Например, при проектировании дорог или строительстве рамп. Зная высоту и длину склона, можно рассчитать угол наклона с помощью тангенса. Это позволяет определить оптимальные параметры для безопасного движения транспорта по дороге или рампе.
Также тангенс может использоваться для расчета прочности конструкций. Например, в строительстве мостов с различными углами наклона опор. Рассчитывая силы, действующие на опоры, можно использовать тангенс для определения оптимальной геометрии опор и материалов, чтобы обеспечить необходимую прочность и безопасность конструкции.
Взаимосвязь тангенса с другими тригонометрическими функциями

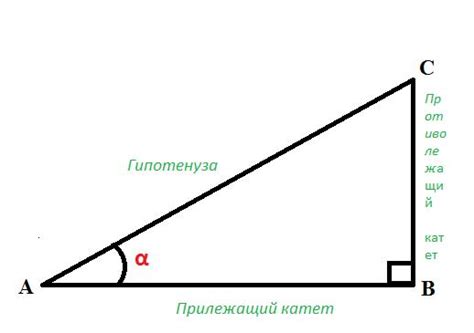
Тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему катету. Формула определения тангенса имеет вид:
tan(A) = a/b,
где A – угол, a – противолежащий катет, b – прилежащий катет.
Из этой формулы можно получить выражение тангенса через синус и косинус:
tan(A) = sin(A) / cos(A).
Это выражение показывает, что тангенс угла равен отношению синуса к косинусу того же угла.
Также можно получить взаимосвязь между тангенсом и синусом:
tan(A) = sin(A) / √(1 - sin²(A)).
Это выражение показывает зависимость тангенса угла от синуса угла.