Треугольник - одна из основных геометрических фигур, которая широко применяется в научных и практических областях. Взаимосвязь различных геометрических элементов треугольника позволяет решать различные математические задачи, в том числе и находить точки пересечения медиан треугольника.
Медианы треугольника - это отрезки, соединяющие вершины треугольника с серединами противолежащих сторон. Точка пересечения медиан называется центром тяжести треугольника, и обозначается буквой G. Она является точкой баланса треугольника и делит каждую медиану в отношении 2:1.
Основная формула для нахождения координат центра тяжести треугольника - это среднее арифметическое координат вершин треугольника. Для каждой координаты x и y центра тяжести G суммируются соответствующие координаты вершин треугольника и делятся на количество вершин.
Алгоритм нахождения точек пересечения медиан треугольника
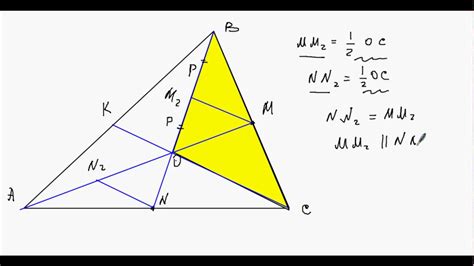
- Найдите координаты вершин треугольника A(x1, y1), B(x2, y2) и C(x3, y3).
- Найдите середины сторон треугольника D((x1+x2)/2, (y1+y2)/2), E((x1+x3)/2, (y1+y3)/2) и F((x2+x3)/2, (y2+y3)/2).
- Найдите уравнения прямых, проходящих через соответствующие вершины и середины противоположных сторон: AD, BE и CF.
- Найдите точки пересечения прямых AD и BE, обозначим данную точку G.
- Найдите точки пересечения прямых AD и CF, обозначим данную точку H.
- Найдите точки пересечения прямых BE и CF, обозначим данную точку I.
Точки G, H и I являются точками пересечения медиан треугольника ABC и совпадают с его центром тяжести.
Таким образом, алгоритм нахождения точек пересечения медиан треугольника заключается в нахождении середин сторон треугольника и нахождении точек пересечения прямых, проходящих через вершины треугольника и середины противоположных сторон. Эти точки являются точками пересечения медиан и центром тяжести треугольника.
Определение медианы треугольника
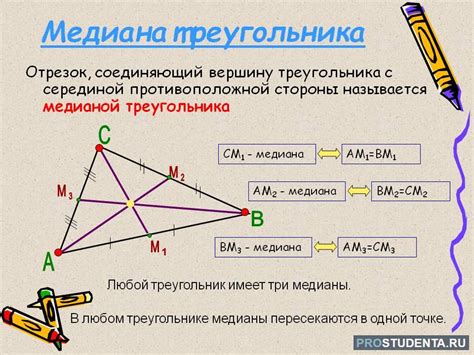
Треугольник имеет три медианы, каждая из которых проходит через одну из вершин и середину противоположной стороны.
Для определения координат точек пересечения медиан треугольника, необходимо знать координаты его вершин.
Медиана проходит через вершину и середину противолежащей стороны, поэтому для вычисления координат точек пересечения медиан треугольника необходимо найти середины всех сторон треугольника.
Для нахождения середины каждой стороны треугольника, нужно суммировать координаты вершин этой стороны и поделить сумму на 2:
(x1 + x2) / 2 и (y1 + y2) / 2 для стороны AB,
(x2 + x3) / 2 и (y2 + y3) / 2 для стороны BC,
(x1 + x3) / 2 и (y1 + y3) / 2 для стороны AC.
Таким образом, точки пересечения медиан треугольника будут иметь координаты, равные серединам соответствующих сторон треугольника.
| Медиана треугольника | Координаты точки пересечения |
|---|---|
| Медиана, проходящая через вершину A | (xAB + xAC) / 2, (yAB + yAC) / 2 |
| Медиана, проходящая через вершину B | (xAB + xBC) / 2, (yAB + yBC) / 2 |
| Медиана, проходящая через вершину C | (xAC + xBC) / 2, (yAC + yBC) / 2 |
Нахождение координат точек пересечения медиан

Для нахождения координат точки пересечения медиан, мы можем воспользоваться формулами, основанными на средних значениях координат вершин треугольника.
Пусть А(x1, y1), В(x2, y2) и С(x3, y3) – координаты вершин треугольника ABC. Тогда координаты точки пересечения медиан вычисляются следующим образом:
x = (x1 + x2 + x3) / 3
y = (y1 + y2 + y3) / 3
Таким образом, мы находим среднее арифметическое по x-координатам и y-координатам всех вершин треугольника, чтобы получить координаты точки пересечения медиан.