Если вы регулярно используете калькулятор для решения математических задач, вам, скорее всего, встречались функции, которые нужно оптимизировать. Чтобы найти точку минимума функции, вам необходимо знать основные шаги алгоритма.
Первым шагом является нахождение производной функции. Производная показвает скорость изменения функции в каждой точке. Чтобы найти точку минимума, вам понадобится найти точку, в которой производная равна нулю. Эта точка будет критической точкой функции.
После нахождения критической точки, следующим шагом является проверка второй производной функции. Если значение второй производной больше нуля, то критическая точка будет точкой минимума. Если значение второй производной меньше нуля, то критическая точка будет точкой максимума функции.
Не забывайте: при нахождении точки минимума функции калькулятора, всегда стоит проверить результат с помощью других методов, таких как графическое представление функции или численные методы. Это поможет вам убедиться в правильности полученного результата и избежать возможных ошибок.
Понятие точки минимума

Для нахождения точки минимума часто применяют различные методы оптимизации, такие как поиск экстремума, градиентный спуск или метод Ньютона. Они позволяют найти точку минимума функции, руководствуясь параметрами и условиями задачи.
Когда находится точка минимума функции, она является критической точкой, где производная функции равна нулю или другим образом меняет свой знак. Это позволяет определить, что функция имеет локальный минимум в этой точке.
Понимание точек минимума функции важно во многих областях, таких как экономика, физика и машинное обучение. Оно позволяет оптимизировать процессы, улучшать результаты и находить оптимальные решения задач.
Примечание: при оптимизации функций с использованием калькулятора необходимо учитывать, что точки минимума функций могут быть условными, то есть зависеть от ограничений и условий задачи.
Что такое точка минимума?
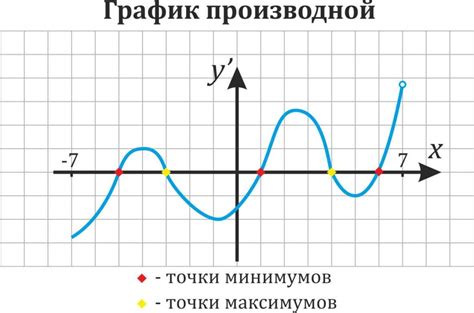
Чтобы найти точку минимума функции, необходимо произвести анализ ее производной. Если производная функции равна нулю в точке, то это может быть точка экстремума функции. Для определения, является ли данная точка минимумом или максимумом, используется вторая производная функции. Если вторая производная больше нуля, то это точка минимума, если меньше нуля - то максимума.
Точка минимума функции является точкой локального или глобального минимума. Локальный минимум - это такая точка, при которой функция достигает наименьшего значения только в некоторой окрестности этой точки. Глобальный минимум - это такая точка, при которой функция достигает наименьшего значения на всем своем домене.
Найти точку минимума функции позволяет определить оптимальные решения для различных задач в физике, экономике, технике и других областях, где необходимо оптимизировать процессы и найти наилучшие значения параметров.
Алгоритмы поиска точки минимума

Один из самых популярных алгоритмов поиска минимума функции - это метод дихотомии (или метод деления пополам). Он основан на принципе деления отрезка пополам и последующем исключении половины отрезка, в которой точка минимума не может находиться. Этот алгоритм эффективен на функциях, которые монотонно убывают или возрастают.
Другой популярный алгоритм - это метод Ньютона, использующий итерации для приближенного нахождения точки минимума. Он основан на теореме о среднем значении и предполагает нахождение корня касательной линии к графику функции.
Кроме того, существуют алгоритмы, использующие генетические алгоритмы и эволюционное моделирование для поиска точки минимума функции. Они основаны на идеях естественного отбора и мутирования, где решения рассматриваются как гены, а лучшие решения сохраняются.
| Алгоритм | Принцип работы | Преимущества | Недостатки |
|---|---|---|---|
| Метод дихотомии | Деление отрезка пополам и исключение половины, в которой точка минимума не может находиться | Прост в реализации, эффективен на монотонных функциях | Неэффективен на функциях с быстрыми колебаниями, требует больше итераций для точного результата |
| Метод Ньютона | Поиск корня касательной линии к графику функции | Быстрая сходимость, точный результат | Требует вычисление производной функции, не всегда сходится к точке минимума |
| Генетические алгоритмы | Использование естественного отбора и мутирования для поиска наилучшего решения | Может находить глобальный минимум, подходит для сложных функций | Требует больше вычислительных ресурсов, не всегда находит точку минимума |
При выборе алгоритма поиска точки минимума функции калькулятора необходимо учитывать особенности самой функции, а также требования к скорости и точности результата. Комбинирование различных алгоритмов и тестирование на разных функциях может помочь найти оптимальное решение.
Градиентный спуск
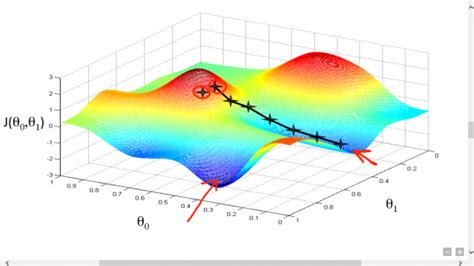
Градиент функции определяется как вектор его частных производных по каждой переменной. Этот вектор указывает направление наибольшего возрастания функции. Чтобы найти локальный минимум функции, градиентный спуск начинает с некоторой начальной точки и шаг за шагом корректирует ее в направлении, противоположном градиенту. Этот процесс повторяется до тех пор, пока не будет достигнута точка, в которой градиент близок к нулю.
Градиентный спуск широко применяется в машинном обучении и оптимизации, где его задача состоит в нахождении параметров модели, при которых достигается минимум функции потерь. Этот метод позволяет эффективно решать сложные задачи оптимизации в больших пространствах параметров.
Метод Ньютона

Для использования метода Ньютона необходимо иметь непрерывно-дифференцируемую функцию, а также начальное приближение точки минимума.
Основная идея метода Ньютона состоит в том, чтобы последовательно находить приближения к точке минимума, используя следующую формулу:
$$x_{n+1} = x_n - \frac{f'(x_n)}{f''(x_n)}$$
где $x_{n+1}$ - новое приближение, $x_n$ - предыдущее приближение, $f'(x_n)$ - первая производная функции в точке $x_n$, $f''(x_n)$ - вторая производная функции в точке $x_n$.
Процесс продолжается до сходимости, то есть до достижения заданной точности или до выполнения критерия останова.
Метод Ньютона обладает быстрой скоростью сходимости, особенно в окрестности точки минимума. Однако он имеет недостаток в том, что требует ручного вычисления производных функции, что может быть затруднительно для сложных функций.
Данный метод широко применяется в оптимизации функций, а также в задачах нахождения корней уравнений.
Метод Бройдена-Флетчера-Гольдфарба-Шанно
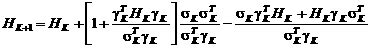
Основная идея метода заключается в том, чтобы аппроксимировать градиент функции и на каждом шаге двигаться в направлении, обратном градиенту. При этом матрица, описывающая изменение градиента на каждом шаге, также изменяется для учета особенностей функции.
На каждой итерации метода вычисляется вектор сдвига, который определяет изменение аргумента функции. Затем находится новая точка, соответствующая этому сдвигу, и производится обновление матрицы переменной метрики. Итерационный процесс повторяется до достижения требуемой точности или заданного числа итераций.
Метод Бройдена-Флетчера-Гольдфарба-Шанно является эффективным и надежным способом нахождения точки минимума функции калькулятора. Он широко применяется в различных областях, таких как оптимизация параметров моделей, настройка алгоритмов машинного обучения и другие задачи, связанные с численной оптимизацией.