Поиск точки пересечения абсцисс двух графиков является одной из основных задач аналитической геометрии. Это позволяет определить значения аргумента, при которых функции пересекаются на координатной плоскости.
Найти точку пересечения абсцисс между двумя графиками можно с помощью простого алгоритма. Сначала необходимо определить уравнения функций, которые задают данные графики. Затем необходимо приравнять значения этих функций и решить полученное уравнение относительно аргумента. Таким образом, найдя значение аргумента, можно найти точку пересечения абсцисс двух графиков.
Примеры точек пересечения абсцисс двух графиков можно найти в различных областях науки и техники. Например, в физике такая задача возникает при определении времени столкновения двух тел, движущихся по разным траекториям. В экономике точка пересечения абсцисс может означать равновесие рыночных цен на товары. В математике задача о поиске точки пересечения абсцисс двух графиков помогает решить уравнения и системы уравнений.
Метод графического решения
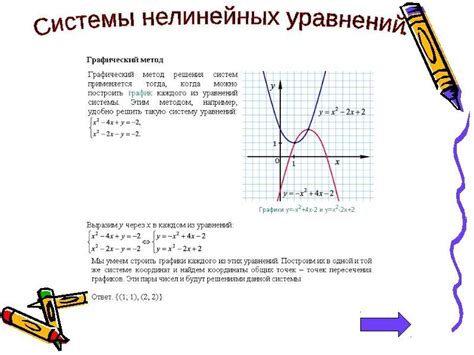
Для применения этого метода необходимо иметь уравнения графиков двух функций, а именно: y = f(x) и y = g(x).
Шаги по применению метода графического решения:
- Задать значения переменной x и найти соответствующие значения y для каждой из функций.
- Построить графики функций на одной плоскости, используя полученные значения.
- Анализировать графики и найти точку пересечения абсцисс. Точка пересечения будет иметь одинаковые значения x для обоих графиков.
Для более точной оценки точки пересечения можно использовать таблицу значений функций. В этом случае необходимо найти значения функций для различных значений x, построить таблицу и проанализировать ее на предмет пересечения абсцисс.
Метод графического решения является относительно простым и позволяет наглядно представить взаимодействие двух функций на плоскости. Однако он не всегда обеспечивает точное решение и может потребовать дополнительных проверок и вычислений.
| Пример | Уравнение графика |
|---|---|
| Пример 1 | y = 2x + 3 |
| Пример 2 | y = x^2 |
В данной таблице представлены два примера уравнений графиков функций. С помощью метода графического решения мы можем построить графики этих функций и определить точку их пересечения на оси абсцисс.
Использование графического решения позволяет наглядно представить результат и облегчает понимание взаимосвязи функций. Однако для точного определения точки пересечения и решения задачи может потребоваться применение дополнительных методов и вычислений.
Решение с использованием аналитических вычислений
Допустим, у нас имеются два графика, заданных уравнениями:
- График 1: y = f(x)
- График 2: y = g(x)
Для нахождения точки пересечения абсцисс, необходимо приравнять выражения f(x) и g(x):
f(x) = g(x)
Теперь у нас есть система уравнений, которую можно решить аналитически, используя различные методы решения систем уравнений, такие как подстановка, метод Гаусса и т.д.
После решения этой системы уравнений мы найдем значение x - точку пересечения абсцисс двух графиков. Это будет являться решением задачи.
Если уравнения графиков заданы в виде таблицы значений или графически, то необходимо восстановить аналитическую зависимость для каждого графика и затем решить систему уравнений аналитически, как описано выше.
Использование аналитических вычислений позволяет точно найти точку пересечения абсцисс двух графиков, обеспечивая надежные результаты для дальнейшего анализа и принятия решений.
Пример нахождения точки пересечения графиков
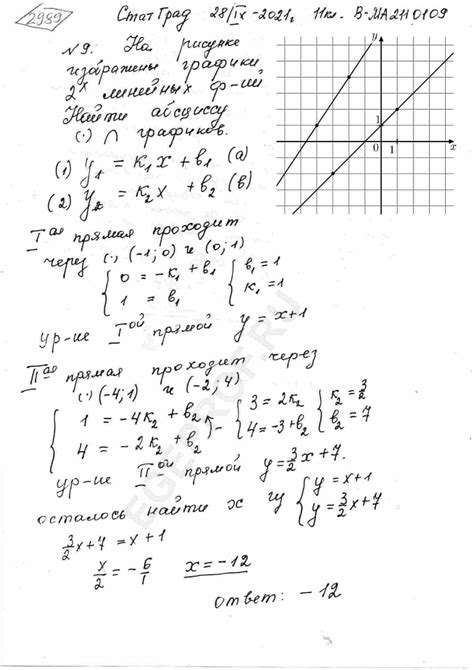
Для нахождения точки пересечения абсцисс двух графиков можно использовать метод графического представления, аналитический метод или численные методы.
Рассмотрим пример нахождения точки пересечения графиков функций y = 2x и y = 5 - x2.
Графический метод:
- Построим графики функций y = 2x и y = 5 - x2 на одном графике.
- Найдем точку пересечения графиков путем визуального анализа.
- Определим координаты точки пересечения.
Аналитический метод:
- Подставим обе функции в уравнение:
- Приведем уравнение к квадратному виду:
- Решим полученное квадратное уравнение для x:
- Найдем соответствующие значения y для найденных x, подставив их обратно в исходные функции:
- Таким образом, точки пересечения графиков - (-3, -6) и (1, 2).
2x = 5 - x2
x2 + 2x - 5 = 0
x = -3 или x = 1
При x = -3: y = 2*(-3) = -6
При x = 1: y = 2*1 = 2
Численные методы:
Для нахождения точки пересечения графиков можно использовать численные методы, такие как метод половинного деления, метод Ньютона и другие. Эти методы позволяют найти приближенное значение точки пересечения с заданной точностью.
Выбор метода нахождения точки пересечения графиков зависит от поставленной задачи, доступных инструментов и желаемой точности результата.
Советы по поиску точки пересечения абсцисс
1. Анализ графиков
Перед началом поиска точки пересечения абсцисс необходимо внимательно изучить два графика, количество пересечений абсцисс которых вы хотите найти. Обратите внимание на их форму и направление. Выявите общий тенденцию поведения графиков при их пересечении.
2. Использование алгебраических методов
Если у вас есть уравнения графиков, можете использовать математические методы для определения точки пересечения абсцисс. Решите систему уравнений, приравняв функции друг к другу и найдите значение переменных, при которых уравнения будут иметь одинаковое значение.
3. Графический метод
Постройте графики функций на одном координатном листе и используйте линейку или другой инструмент, чтобы определить точку пересечения графиков на оси абсцисс. Будьте внимательны и точны при измерениях, чтобы получить более точный результат.
4. Использование математических программ и калькуляторов
Современные математические программы и калькуляторы часто позволяют найти точку пересечения абсцисс графиков автоматически. Вам просто нужно ввести уравнения или задать функции и программное обеспечение самостоятельно решит задачу для вас. Однако не забывайте проверять результаты на понятность и корректность.
5. Перебор значений абсцисс
Если у вас нет математических методов или программного обеспечения для поиска точки пересечения абсцисс, вы можете попробовать перебирать различные значения абсцисс в области пересечения графиков. Подберите значения, начиная с наименьшего и увеличивая их постепенно, пока не найдете сходство в значениях функций.
Не забывайте, что поиск точки пересечения абсцисс может быть неточным и требует внимательности и аккуратности. В случае сложных функций или неоднозначных результатов, рекомендуется использовать более точные численные и математические методы.