Точка пересечения прямой с осями координат – это особенный случай в математике, который позволяет определить координаты точки, где прямая пересекает оси плоскости. Знание этого метода может быть полезно во многих областях, от физики и геометрии до экономики и программирования.
Существуют различные методы определения точки пересечения прямой с осями координат. Один из наиболее простых и распространенных методов – это уравнение прямой в виде y = kx + b. В этом случае, чтобы найти точку пересечения с осью x, нужно приравнять y к нулю и решить уравнение для x. Аналогично, чтобы найти точку пересечения с осью y, нужно приравнять x к нулю и решить уравнение для y.
Для более сложных случаев, когда уравнение прямой имеет вид Ax + By = C, можно использовать методы сложения и вычитания уравнений. Они позволяют найти значения x и y, при которых оба уравнения равны. Эти значения будут координатами точки пересечения прямой с осями координат.
В данной статье мы рассмотрим примеры использования этих методов для нахождения точки пересечения прямой с осями координат. Также мы рассмотрим особые случаи, когда прямая параллельна одной из осей или проходит через начало координат.
Методы нахождения точки пересечения прямой с осями координат
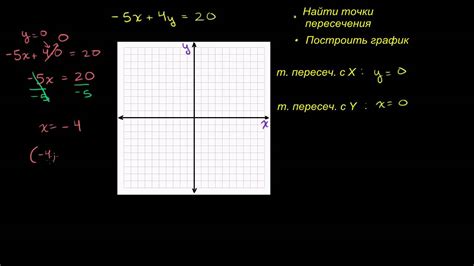
1. Аналитический метод
Аналитический метод основан на использовании уравнения прямой и равенства координат точки пересечения с осями координат.
1.1. Для нахождения точки пересечения с осью абсцисс (ось X) необходимо приравнять значение ординаты (Y) к нулю и решить уравнение по координате X.
1.2. Для нахождения точки пересечения с осью ординат (ось Y) необходимо приравнять значение абсциссы (X) к нулю и решить уравнение по координате Y.
Применение аналитического метода требует знания уравнения прямой и умения решать линейные уравнения. Для примера, рассмотрим прямую с уравнением Y = 3X + 2.
1.1. По условию задачи, чтобы найти точку пересечения с осью абсцисс (то есть точку с координатой Y = 0), подставим Y = 0 в уравнение и решим полученное уравнение по X: 0 = 3X + 2. Выразив X, получим X = -2/3.
1.2. Чтобы найти точку пересечения с осью ординат (то есть точку с координатой X = 0), подставим X = 0 в уравнение и решим полученное уравнение по Y: Y = 3 * 0 + 2. Получим Y = 2.
Значит, точка пересечения прямой с осями координат для данного примера имеет координаты (-2/3, 0) и (0, 2).
2. Графический метод
Графический метод нахождения точки пересечения прямой с осями координат основан на построении графика прямой на координатной плоскости и определении точек пересечения с осями.
2.1. Чтобы найти точку пересечения с осью абсцисс, построим график прямой на координатной плоскости и определим точку, в которой график пересекает ось абсцисс.
2.2. Чтобы найти точку пересечения с осью ординат, построим график прямой на координатной плоскости и определим точку, в которой график пересекает ось ординат.
Графический метод является визуальным и простым в использовании. Он позволяет наглядно представить точки пересечения прямой с осями координат и, при необходимости, произвести дополнительные измерения для получения точных значений координат.
В конечном итоге, какой метод использовать для нахождения точки пересечения прямой с осями координат зависит от задачи и предпочтений решателя. Аналитический метод обладает точностью и формальностью, в то время как графический метод является более наглядным и простым в использовании.
Аналитический метод нахождения точки пересечения

Аналитический метод нахождения точки пересечения прямой с осями координат на плоскости основан на решении системы уравнений, состоящей из уравнения прямой и уравнений осей координат.
Пусть уравнение прямой имеет вид y = kx + b, где k - коэффициент наклона, b - коэффициент сдвига по оси y.
Чтобы найти точку пересечения прямой с осью x (абсциссой), можно подставить y = 0 в уравнение прямой и решить полученное уравнение относительно x. Полученное значение x будет абсциссой точки пересечения с осью x.
Аналогично, чтобы найти точку пересечения прямой с осью y (ординатой), можно подставить x = 0 в уравнение прямой и решить полученное уравнение относительно y. Полученное значение y будет ординатой точки пересечения с осью y.
Приведем пример: рассмотрим прямую с уравнением y = 2x + 3.
Для нахождения точки пересечения с осью x, подставим y = 0 и решим уравнение:
- 0 = 2x + 3
- 2x = -3
- x = -3/2
Таким образом, получаем, что точка пересечения с осью x имеет координаты (-3/2, 0).
Для нахождения точки пересечения с осью y, подставим x = 0 и решим уравнение:
- y = 2 * 0 + 3
- y = 3
Таким образом, получаем, что точка пересечения с осью y имеет координаты (0, 3).
Таким образом, аналитический метод позволяет найти точку пересечения прямой с осями координат на плоскости, опираясь на уравнение прямой и уравнения осей координат.
Графический метод нахождения точки пересечения

Чтобы найти точку пересечения прямой с осью OX, необходимо найти точку, в которой прямая пересекает горизонтальную ось. Для этого мы откладываем от начала координат (0, 0) по горизонтальной оси нужное значение по оси X и проводим от этой точки перпендикуляр к оси OX. Точка пересечения этого перпендикуляра с осью OX и будет являться искомой точкой пересечения прямой с осью.
Аналогично, чтобы найти точку пересечения прямой с осью OY, нужно найти точку, в которой прямая пересекает вертикальную ось. Для этого от начала координат откладываем по вертикальной оси нужное значение по оси Y и проводим от этой точки перпендикуляр к оси OY. Точка пересечения перпендикуляра с осью OY будет точкой пересечения прямой с осью.
Графический метод нахождения точки пересечения прямой с осями координат особенно удобен в задачах, где необходимо найти точку пересечения двух прямых или наличие пересечения прямой с осями, так как он позволяет визуально представить решение и более наглядно интерпретировать результаты.