На рисунке 47, изображены две прямые ab и cd, и вам нужно найти точку их пересечения. Это может быть полезно в различных ситуациях, например, при решении геометрических задач или анализе данных. Но как это сделать?
Существует несколько способов найти точку пересечения прямых ab и cd. Один из самых простых и популярных методов - использование системы уравнений. Прямая ab может быть представлена уравнением ax + by = c, а прямая cd - cx + dy = f. Решив эту систему уравнений, вы получите координаты точки пересечения.
Еще один способ - использование графического метода. Для этого нужно построить график каждой из прямых и найти их точку пересечения. Для этого необходимо найти значения x и y, при которых уравнения прямых равны друг другу. Это может быть выполнено графически или с использованием математических методов, таких как метод подстановки или метод Крамера.
Чтобы найти точку пересечения прямых ab и cd на рисунке 47, необходимо выбрать метод, который вам наиболее понятен и удобен. Имейте в виду, что в некоторых случаях прямые могут быть параллельными или совпадающими, и точка пересечения может быть не найдена. В таких случаях методы поиска точки пересечения могут не применяться, и вам может потребоваться другой подход к решению задачи.
Анализ рисунка 47 и определение координат точек
Рисунок 47 представляет собой графическое изображение двух пересекающихся прямых ab и cd на плоскости. Для определения точки пересечения этих прямых необходимо проанализировать рисунок и определить их координаты.
Для начала, необходимо определить оси координат. Обычно наиболее распространенная система координат - прямоугольная. На данном рисунке можно предположить, что внизу изображены оси X и Y, горизонтальная и вертикальная оси соответственно. Для наглядности обозначим ось X горизонтальной линией и ось Y - вертикальной линией.
Далее, следует анализировать изображенные прямые ab и cd. Прямая ab, как правило, обозначается с помощью двух точек - начальной и конечной. В данном случае, начальная точка обозначена как a, а конечная - точкой b. Аналогично, для прямой cd начальная и конечная точки обозначены как c и d соответственно.
Для определения координат точки пересечения прямых ab и cd на рисунке 47, необходимо найти точку, в которой они пересекаются. Обычно такая точка обозначается буквой O. Для того чтобы определить координаты точки O, можно использовать различные методы, такие как аналитическая геометрия или построение графиков. При использовании аналитической геометрии, можно решить систему уравнений, составленных для прямых ab и cd, и получить координаты точки O.
Итак, осуществив анализ рисунка 47 и определив оси координат, начальные и конечные точки прямых ab и cd, можно приступить к нахождению координат точки пересечения этих прямых. Для этого можно воспользоваться методами аналитической геометрии или построения графиков.
Определение координаты точки a
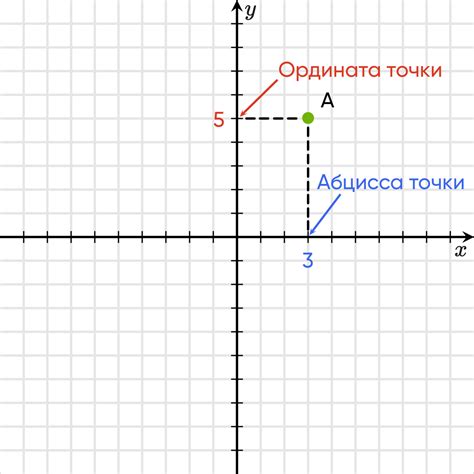
Координата точки a может быть определена путем нахождения точки пересечения прямых ab и cd на рисунке 47.
Для этого можно воспользоваться уравнениями данных прямых и решить систему уравнений для неизвестных координат точки a. Обычно прямые задаются в виде уравнений вида y = kx + b, где k - наклон прямой, b - свободный член. Подставив две эти уравнения, можно найти координаты точки пересечения, которые и будут координатами точки a.
Для удобства можно представить уравнения прямых в виде общего уравнения прямой Ax + By + C = 0. Путем решения системы уравнений можно найти значения A, B и C для обеих прямых ab и cd. Подставив эти значения в уравнения прямых и решив систему, можно получить координаты точки a.
Определение координаты точки a позволяет понять, где именно находится данная точка на рисунке 47 и использовать ее для дальнейших вычислений или конструкций.
Определение координаты точки b
Для определения координаты точки b на рисунке 47, необходимо использовать уравнения прямых ab и cd и решить их систему.
Уравнение прямой ab можно записать в виде y = kx + b, где k - коэффициент наклона прямой, а b - свободный коэффициент. Аналогично, уравнение прямой cd записывается как y = mх + c, где m и c - соответствующие коэффициенты.
Зная уравнения прямых ab и cd, необходимо решить систему этих уравнений. Решение этой системы даст значения x и y, которые являются координатами точки b.
Пример решения системы уравнений:
- Записываем уравнения прямых ab и cd:
ab: y = 2x + 3
cd: y = -3x + 5
- Исключаем переменную y, выражая ее через x из одного из уравнений. Например, из уравнения ab:
y = 2x + 3
- Подставляем это выражение во второе уравнение, получаем:
-3x + 5 = 2x + 3
- Решаем получившееся уравнение, находим значение x:
-5x = -2
x = -2 / -5 = 2/5
- Подставляем найденное значение x в уравнение, чтобы найти значение y:
y = 2 * (2/5) + 3
y = 4/5 + 3
y = 19/5
- Поэтому, координаты точки b равны: (2/5, 19/5)
Таким образом, зная уравнения прямых ab и cd и решив систему этих уравнений, можно определить координаты точки b на рисунке 47.
Определение координаты точки c
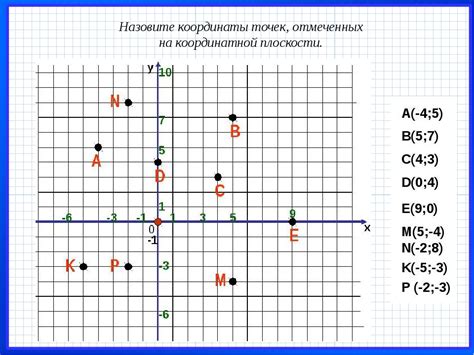
Шаг 1: Определить уравнения прямых ab и cd в координатах. Уравнение прямой можно записать в виде y = mx + b, где m - коэффициент наклона прямой, b - коэффициент свободного члена.
Шаг 2: Подставить координаты точки a в уравнение прямой ab и найти значение y. Аналогично, подставить координаты точки c в уравнение прямой cd и найти значение y.
Шаг 3: Сравнить значения y для точек a и c. Если они совпадают, то точка c лежит на пересечении прямых ab и cd. Если значения y различаются, точка c не является пересечением данных прямых.
Шаг 4: Подставить найденное значение y в любое из уравнений прямых ab или cd и найти соответствующее значение x. Таким образом, мы получим координаты точки c.
Таким образом, следуя указанным шагам, можно определить координату точки c, которая является пересечением прямых ab и cd на рисунке 47.
Определение координаты точки d
Для определения координаты точки d, необходимо использовать информацию о прямых ab и cd на рисунке 47.
Для начала, обратимся к уравнениям данных прямых:
| Прямая | Уравнение |
|---|---|
| ab | y = mx + c |
| cd | y = nx + d |
Здесь m и n - коэффициенты наклона прямых ab и cd соответственно, а c и d - свободные члены. Зная уравнения прямых исходя из рисунка, можно составить систему уравнений:
Система уравнений:
система уравнений
Решая данную систему уравнений, мы найдем значения переменных x и y, которые совпадают с координатами точки пересечения прямых ab и cd, то есть координатами точки d.
Таким образом, определив значения переменных x и y, можно найти координату точки d и использовать ее при необходимости в дальнейших расчетах или построениях.
Уравнение прямых ab и cd
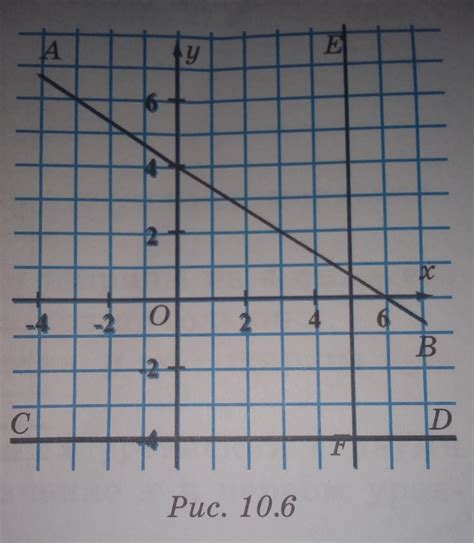
1. Прямая ab: Из рисунка видно, что точка a имеет координаты (xa, ya), а точка b - (xb, yb). Подставив эти значения в уравнение прямой получим:
| Уравнение прямой ab: | y = kabx + bab |
|---|---|
| Точка a: | ya = kabxa + bab |
| Точка b: | yb = kabxb + bab |
2. Прямая cd: Аналогично, точка c имеет координаты (xc, yc), а точка d - (xd, yd). Подставив эти значения в уравнение прямой получим:
| Уравнение прямой cd: | y = kcdx + bcd |
|---|---|
| Точка c: | yc = kcdxc + bcd |
| Точка d: | yd = kcdxd + bcd |
3. Найдем точку пересечения прямых ab и cd, решив систему уравнений:
| Система уравнений: | y = kabx + bab y = kcdx + bcd |
|---|
4. Решение системы уравнений даст значения координат точки пересечения прямых ab и cd. Эти значения можно подставить в уравнение прямой для проверки.
Таким образом, для нахождения точки пересечения прямых ab и cd на рисунке 47 необходимо составить уравнения этих прямых и решить систему уравнений.
Уравнение прямой ab

Для нахождения углового коэффициента m можно воспользоваться формулой:
m = (y2 - y1) / (x2 - x1)
где (x1, y1) и (x2, y2) - координаты двух точек на прямой ab.
Свободный член c можно найти, подставив координаты одной из точек в уравнение прямой:
y - mx = c
Или введя значения координат и находя c по формуле:
c = y - mx
Таким образом, зная угловой коэффициент m и свободный коэффициент c, мы можем записать уравнение прямой ab.
| Уравнение | Формула |
|---|---|
| Угловой коэффициент | m = (y2 - y1) / (x2 - x1) |
| Свободный коэффициент | c = y - mx |
| Уравнение прямой ab | y = mx + c |