Нахождение точки пересечения прямых является одной из важных задач в геометрии. В 7 классе ученики начинают изучать уравнения прямых и разные способы их решения. Знание этих методов поможет им успешно справляться с подобными задачами и строить графики линейных уравнений.
Для того чтобы найти точку пересечения двух прямых, необходимо знать их уравнения. Важно понимать, что прямая задается уравнением вида y = kx + b, где k - это угловой коэффициент, а b - свободный член. Для определения точки пересечения двух прямых необходимо решить систему уравнений, состоящую из уравнений данных прямых. Угловой коэффициент и свободный член каждой прямой нужно подставить в уравнение другой прямой, после чего получится система с двумя уравнениями. Решая эту систему, можно найти координаты точки пересечения и описать ее геометрическое положение на плоскости.
Существуют различные способы решения задач на нахождение точки пересечения прямых. Один из них - графический метод. Для его применения необходимо построить графики данных прямых на координатной плоскости и определить точку пересечения. Данный метод отлично подходит для визуализации решения и позволяет ученику лучше понять геометрическое значение точки пересечения.
Примеры

Вот несколько примеров решения задач на нахождение точки пересечения прямых:
Пример 1:
Даны две прямые: y = 2x + 1 и y = -3x + 4. Найдем их точку пересечения. Для этого приравняем выражения для y:
2x + 1 = -3x + 4
Перегруппируем слагаемые:
2x + 3x = 4 - 1
5x = 3
Разделим обе части уравнения на 5:
x = 3/5
Подставим значение x в одно из начальных уравнений, например, в уравнение y = 2x + 1:
y = 2 * (3/5) + 1
y = 6/5 + 1
Найдем общий знаменатель и сложим дроби:
y = 6/5 + 5/5
y = 11/5
Таким образом, точка пересечения прямых имеет координаты x = 3/5 и y = 11/5.
Пример 2:
Даны две прямые: y = -2x - 3 и y = 4x + 2. Для нахождения точки пересечения приравняем выражения для y:
-2x - 3 = 4x + 2
Перегруппируем слагаемые:
-2x - 4x = 2 + 3
-6x = 5
Разделим обе части уравнения на -6:
x = -5/6
Подставим значение x в одно из начальных уравнений, например, в уравнение y = -2x - 3:
y = -2 * (-5/6) - 3
y = 10/6 - 18/6
Вычтем дроби:
y = (10 - 18)/6
y = -8/6
Упростим дробь, поделив числитель и знаменатель на их общий делитель 2:
y = -4/3
Таким образом, точка пересечения прямых имеет координаты x = -5/6 и y = -4/3.
Пример 3:
Даны две прямые: y = 3x + 2 и y = -x + 5. Приравним выражения для y:
3x + 2 = -x + 5
Перегруппируем слагаемые:
3x + x = 5 - 2
4x = 3
Разделим обе части уравнения на 4:
x = 3/4
Подставим значение x в одно из начальных уравнений, например, в уравнение y = 3x + 2:
y = 3 * (3/4) + 2
y = 9/4 + 8/4
y = 17/4
Таким образом, точка пересечения прямых имеет координаты x = 3/4 и y = 17/4.
Решение задач

Для решения задач на нахождение точки пересечения прямых необходимо знать основные понятия и методы работы с уравнениями прямых.
1. Начнем с определения уравнения прямой в декартовой системе координат. Уравнение прямой имеет вид y = kx + b, где k - коэффициент наклона прямой, b - свободный член уравнения.
2. Для нахождения точки пересечения двух прямых необходимо приравнять их уравнения и решить получившуюся систему уравнений относительно переменных x и y. Получившиеся значения x и y будут координатами точки пересечения.
3. Рассмотрим пример. Даны две прямые: y = 2x + 1 и y = -3x - 2. Найдем их точку пересечения.
| Уравнение прямой | x | y |
|---|---|---|
| y = 2x + 1 | ||
| y = -3x - 2 |
Подставим уравнение первой прямой во второе уравнение:
| Уравнение прямой | x | y |
|---|---|---|
| y = 2x + 1 | ||
| (2x + 1) = -3x - 2 |
Решим получившееся уравнение относительно x:
| Уравнение прямой | x | y |
|---|---|---|
| y = 2x + 1 | ||
| (2x + 1) = -3x - 2 | ||
| 5x = -3 | ||
| x = -3/5 |
Теперь найдем значение y, подставив x в любое из исходных уравнений. Возьмем первое уравнение:
| Уравнение прямой | x | y |
|---|---|---|
| y = 2x + 1 | -3/5 | |
| (-3/5) = 2*(-3/5) + 1 | ||
| -3/5 = -6/5 + 1 | ||
| -3/5 = -6/5 + 5/5 | ||
| -3/5 = -1/5 |
Получившаяся система уравнений не имеет решения, значит прямые не пересекаются и точки пересечения нет.
Таким образом, для решения задач на нахождение точки пересечения прямых необходимо знать основные понятия и методы работы с уравнениями прямых, а также уметь решать системы уравнений.
Нахождение точки пересечения
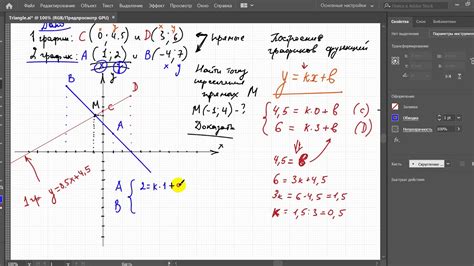
Существует несколько способов нахождения точки пересечения прямых. Один из самых простых и широко используемых методов - это решение системы уравнений с помощью метода замены или метода сложения/вычитания.
Для нахождения точки пересечения двух прямых необходимо иметь их уравнения. Уравнение прямой можно записать в виде у = kx + b, где k - коэффициент наклона прямой, а b - свободный член.
Пример задачи на нахождение точки пересечения:
- Найти точку пересечения прямых, заданных уравнениями:
- 1) y = 2x + 1
- 2) y = 3x - 2
Решение:
Для начала подставим одно уравнение в другое и решим полученную систему:
2x + 1 = 3x - 2
Перенесем все члены с x в левую часть уравнения:
2x - 3x = -2 - 1
-x = -3
Разделим обе части уравнения на -1, чтобы получить x:
x = 3
Теперь найдем y, подставив найденное значение x в любое из уравнений:
y = 2(3) + 1
y = 6 + 1
y = 7
Таким образом, точка пересечения прямых имеет координаты (3, 7).
Этот метод решения задачи нахождения точки пересечения прямых можно применять для любых уравнений прямых.
Прямые
Уравнение прямой в общем виде имеет вид ax + by = c, где a и b – коэффициенты, а c – свободный член. Если прямая вертикальная (параллельна оси OY), то уравнение будет иметь вид x = k, где k – координата на оси OX. Если прямая горизонтальная (параллельна оси OX), то уравнение примет вид y = k.
Однако наиболее распространенным способом задания прямой является указание двух точек, через которые она проходит. Зная координаты этих двух точек, можно восстановить уравнение прямой с использованием формулы y - y1 = ((y2 - y1) / (x2 - x1)) * (x - x1), где (x1, y1) и (x2, y2) – координаты двух точек.
Важной задачей геометрии является нахождение точки пересечения двух прямых. Для этого необходимо решить систему уравнений, состоящую из уравнений данных прямых. Полученные значения координат точки пересечения позволяют определить ее положение относительно прямых (находится ли точка на прямой, между прямыми или вне их).
Знание основных свойств и способов задания прямых позволяет решать задачи, связанные с определением расстояния между прямыми, построением перпендикуляров и параллельных прямых, а также нахождением углов между ними.
Уравнения
Уравнения помогают решать различные задачи, в том числе и определение точки пересечения прямых.
Уравнения прямых представляют собой математические выражения, описывающие прямую линию на плоскости.
В общем виде уравнение прямой можно представить в виде y = mx + b, где y - значение на оси ординат, x - значение на оси абсцисс,
m - коэффициент наклона прямой, b - свободный член уравнения.
Для определения точки пересечения двух прямых необходимо решить систему уравнений, составленную из уравнений прямых.
Решение системы позволит найти значения x и y, соответствующие точке пересечения прямых.
Для этого можно использовать различные методы: метод подстановки, метод сложения или вычитания, метод определителей и другие.
Пример задачи на нахождение точки пересечения прямых:
Найти точку пересечения прямых с уравнениями y = 2x + 1 и y = 3x - 2.
Решение:
Составляем систему уравнений:
{ y = 2x + 1
{ y = 3x - 2
Методом вычитания находим значение x:
2x + 1 = 3x - 2
x = 3
Подставляем найденное значение x в любое из уравнений, например в y = 2x + 1:
y = 2*3 + 1
y = 7
Точка пересечения прямых имеет координаты (3, 7).
Ответ: Точка пересечения прямых имеет координаты (3, 7).
Способы
Существует несколько способов решения задач на нахождение точки пересечения прямых.
- Метод подстановки: подставляем значения координат точки в оба уравнения прямых и проверяем их равенство. Если равенство выполняется, то координаты точки являются решением системы уравнений, и она является точкой пересечения прямых.
- Метод вычитания: вычитаем одно уравнение прямой из другого, чтобы устранить неизвестное и найти координаты точки пересечения.
- Метод подобных треугольников: находим угловой коэффициент прямых и используем его, чтобы найти координаты точки пересечения.
- Метод графического представления: строим графики уравнений прямых на координатной плоскости и находим точку их пересечения.
Выбор способа решения задачи зависит от ее условий и предпочтений ученика. Важно понимать принципы и особенности каждого способа, чтобы успешно решать задачи на нахождение точки пересечения прямых.
Класс 7

В 7 классе ученики начинают изучать математику более глубоко и систематически. Тема ординат особенно важна для их дальнейшего понимания графиков и анализа данных.
Одной из важных тем в 7 классе является нахождение точки пересечения прямых. Для этого необходимо знать уравнения этих прямых и правила их решения. В основном учатся находить точку пересечения, если уравнения прямых даны в виде y = kx + b, где k - коэффициент наклона прямой, а b - свободный член уравнения.
Примером задачи может служить следующая: "Найти точку пересечения прямых y = 2x + 3 и y = -3x + 6". Чтобы решить эту задачу, необходимо приравнять уравнения прямых и решить получившееся уравнение относительно x. После нахождения значения x подставляем его в одно из уравнений и находим соответствующее значение y. Таким образом, мы получаем координаты точки пересечения.
Решая подобные задачи, ученик тренирует свои навыки работы с алгебраическими уравнениями, анализа графиков и логического мышления. Применение этих знаний позволяет решать задачи из реальной жизни, связанные с поиском пересечений двух прямых или соединений точек в декартовой системе координат.
Изучение точек пересечения прямых в 7 классе является важным этапом в формировании математической базы ученика, которая дальше будет использоваться в анализе графиков функций и решении более сложных алгебраических задач.