Точка пересечения точки и прямой - это математическое понятие, которое определяет местоположение точки на плоскости, где она пересекает заданную прямую. Это важный элемент в геометрии и аналитической геометрии, который используется для решения множества задач и проблем.
Существует несколько методов для определения точки пересечения точки и прямой. Одним из них является метод подстановки. При использовании этого метода необходимо заменить координаты точки в уравнение прямой и решить полученное уравнение относительно неизвестных переменных. Таким образом, мы можем найти координаты точки пересечения.
Другим методом является метод графического изображения. Для этого необходимо построить график прямой и точки на одной плоскости. Точка пересечения будет являться точкой, в которой прямая и точка пересекаются.
Давайте рассмотрим пример:
У нас есть прямая, заданная уравнением: y = 2x + 3. Требуется найти точку пересечения этой прямой с точкой А(4, 7).
Метод подстановки:
Подставим координаты точки A в уравнение прямой:
7 = 2 * 4 + 3
7 = 8 + 3
7 = 11
Таким образом, точка А(4, 7) не является точкой пересечения прямой и точки.
Метод графического изображения:
Построим график прямой y = 2x + 3 и точку А(4, 7) на координатной плоскости.
[Иллюстрация: график прямой и точка]
Как видно из графика, прямая и точка А не пересекаются, следовательно, точка А(4, 7) не является точкой пересечения прямой и точки.
Таким образом, наш анализ показал, что точка А(4, 7) не является точкой пересечения прямой и точки. В зависимости от задачи и данных условий, методы определения точки пересечения могут отличаться. Важно учитывать особенности каждого метода и выбирать наиболее подходящий для решения конкретной задачи.
Метод аналитической геометрии
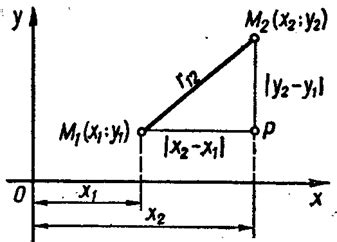
Чтобы найти точку пересечения, необходимо знать уравнения данной прямой и заданной точки. Уравнение прямой может быть дано в различных формах, таких как уравнение прямой в общем виде, каноническое уравнение прямой или уравнение прямой в параметрической форме.
После того, как уравнения прямой и точки известны, можно решить систему уравнений, состоящую из уравнения прямой и уравнения, описывающего точку. Решением этой системы будут значения координат точки пересечения.
Например, пусть у нас есть прямая с уравнением y = 2x + 1 и точка с координатами (3, 7). Чтобы найти точку пересечения, подставим значения координат точки в уравнение прямой:
y = 2x + 1
7 = 2 * 3 + 1
7 = 7
Получили равенство, значит, точка (3, 7) лежит на данной прямой и является точкой пересечения.
Метод аналитической геометрии позволяет найти точку пересечения точки и прямой с использованием алгебраических методов. Он является одним из эффективных инструментов для решения задач, связанных с нахождением пересечений на плоскости.
Метод графического представления

Для использования данного метода необходимо иметь график точки и график прямой. График точки представляется в виде отдельной точки на плоскости, а график прямой - в виде линии, заданной уравнением прямой.
Чтобы найти точку пересечения, необходимо визуально определить место, где график точки и график прямой пересекаются. Это будет точка пересечения точки и прямой.
Пример 1: Имеется точка A(3, 5) и прямая с уравнением y = 2x - 1. Чтобы найти точку пересечения, нужно построить график точки A и график прямой на плоскости. После этого визуально определить точку пересечения.
Пример 2: Имеется точка B(1, 4) и прямая с уравнением y = -3x + 6. Аналогично предыдущему примеру, нужно построить график точки B и график прямой на плоскости, а затем визуально найти точку пересечения.
Метод графического представления позволяет найти точку пересечения точки и прямой достаточно быстро и наглядно для любого уровня математической подготовки.
Иллюстрированный пример с расчетами
Представим, что у нас есть прямая линия с уравнением y = 2x + 3 и точка P с координатами (2, 7). Мы хотим найти точку пересечения прямой и точки.
Шаг 1: Найдем уравнение прямой, проходящей через точку P. Заменим значения x и y в уравнении прямой на координаты точки P:
7 = 2 * 2 + 3
Шаг 2: Решим уравнение, чтобы найти значение x:
7 - 3 = 2 * x
4 = 2 * x
x = 2
Шаг 3: Подставим найденное значение x в уравнение прямой, чтобы найти значение y:
y = 2 * 2 + 3 = 7
Таким образом, точка пересечения прямой и точки P имеет координаты (2, 7), что и является ответом на нашу задачу.
Проблемы и сложности при нахождении точки пересечения
Нахождение точки пересечения может быть сложной задачей, особенно при работе с прямыми, имеющими различные наклоны и координаты начальных точек. Важно учитывать следующие проблемы и сложности при решении данной задачи:
Сложности с графическим представлением: визуальное определение точки пересечения прямой и прямой на графике может быть непростой задачей, особенно если прямые имеют похожие уровни наклона или пересекаются в области графика с большим количеством других линий.
Затруднения с аналитическим подходом: при решении задачи математически и аналитически необходимо учесть различные формулы и уравнения прямых в пространстве, их системы и переменные, что может быть трудно понять и применить в конкретной ситуации.
Неоднозначность исходных данных: иногда исходные данные могут быть неоднозначными или неполными, что делает точное определение точки пересечения сложным или даже невозможным. Необходимо проводить проверку и дополнение данных перед решением задачи.
Ошибки при вычислениях: при рассчете точки пересечения прямых могут возникать ошибки, связанные с округлением чисел, сокращением или пропуском действий в вычислениях и другими факторами. Важно быть внимательным и аккуратным при выполнении вычислительных операций.
Сложности с программированием: при автоматизации расчетов и определения точки пересечения прямых с помощью программных средств возникают свои сложности, связанные с выбором и реализацией алгоритмов и методов работы с данными.
Учитывая данные проблемы и сложности, важно проявлять терпение и внимательность при решении задачи нахождения точки пересечения и обращаться к графическому или аналитическому методу в зависимости от конкретной ситуации.