Прямоугольные треугольники - одна из самых интересных и полезных геометрических форм. И одним из ключевых аспектов работы с ними является определение длины третьей стороны. Зачастую возникает необходимость найти ее длину, когда известны только длины двух других сторон. В этой статье мы рассмотрим формулу и приведем примеры, которые помогут вам в этом вопросе.
Формула, позволяющая найти длину третьей стороны прямоугольного треугольника, называется "теоремой Пифагора". Она основана на том, что квадрат длины гипотенузы (сторона прямоугольного треугольника, лежащая напротив прямого угла) равен сумме квадратов длин катетов (двух оставшихся сторон).
Если обозначить гипотенузу буквой c, а катеты - a и b, то формула теоремы Пифагора будет выглядеть так: c^2 = a^2 + b^2. Для того чтобы найти длину гипотенузы, нужно извлечь квадратный корень из обеих сторон уравнения, получив такую формулу: c = √(a^2 + b^2).
Формула для нахождения третьей стороны прямоугольного треугольника
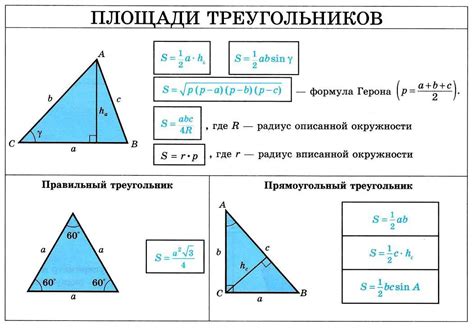
Формула для нахождения третьей стороны прямоугольного треугольника основана на теореме Пифагора. Суть этой теоремы заключается в следующем: квадрат длины гипотенузы (стороны, напротив прямого угла) равен сумме квадратов длин двух катетов (остальных двух сторон).
Таким образом, если известны длины катетов a и b, то длина гипотенузы c может быть найдена по формуле:
c = √(a² + b²)
Где √ обозначает квадратный корень.
Например, если известны длины катетов a = 3 и b = 4, то используя формулу, мы можем найти длину гипотенузы:
c = √(3² + 4²) = √(9 + 16) = √25 = 5
Таким образом, третья сторона прямоугольного треугольника равна 5.
Примеры использования формулы
Вот несколько примеров, чтобы наглядно продемонстрировать, как использовать формулу для нахождения третьей стороны прямоугольного треугольника:
Пример 1:
Известны стороны прямоугольного треугольника A = 3 и B = 4. Чтобы найти сторону C, используем формулу C = √(A² + B²):
C = √(3² + 4²) = √(9 + 16) = √25 = 5.
Таким образом, третья сторона прямоугольного треугольника равна 5.
Пример 2:
Известны стороны прямоугольного треугольника A = 5 и B = 12. Чтобы найти сторону C, снова используем формулу C = √(A² + B²):
C = √(5² + 12²) = √(25 + 144) = √169 = 13.
Следовательно, третья сторона прямоугольного треугольника равна 13.
Пример 3:
Известны стороны прямоугольного треугольника A = 8 и B = 15. Снова используем формулу C = √(A² + B²):
C = √(8² + 15²) = √(64 + 225) = √289 = 17.
Таким образом, третья сторона прямоугольного треугольника равна 17.
Помните, что формула C = √(A² + B²) применяется только в случае прямоугольного треугольника, где A и B - это длины катетов, а C - это длина гипотенузы.