У равнобедренного треугольника две равные стороны и два равных угла. Вам известен один угол равнобедренного треугольника, и это 40 градусов. Но как найти остальные углы?
Первым шагом является определение величины равных углов. Так как треугольник равнобедренный, у него два равных угла. Поэтому для начала узнаем, какова величина каждого из них.
Чтобы найти величину каждого из равных углов, необходимо использовать свойство равнобедренного треугольника. Это свойство заключается в том, что каждый из равных углов равен половине дополнительного угла, который составляет 180 градусов минус угол равнобедренного треугольника. В данном случае угол равнобедренного треугольника равен 40 градусов. Будем обозначать величину каждого из равных углов буквой "х".
Определение углов равнобедренного треугольника
Очень часто, чтобы найти углы равнобедренного треугольника, необходимо знать значение одного из углов. В этой статье мы рассмотрим случай, когда известно, что один из углов равен 40 градусов.
Чтобы найти остальные углы равнобедренного треугольника, нужно воспользоваться свойством треугольника, согласно которому сумма всех углов треугольника равна 180 градусов.
Так как два угла равнобедренного треугольника одинаковы и равны между собой, то мы можем представить треугольник как два равносторонних треугольника, соединенных основаниями, которые являются равными сторонами равнобедренного треугольника.
Рассмотрим равносторонний треугольник, известно что один угол в нем равен 40 градусов. Значит другие два угла также равны и имеют одинаковую величину.
Сумма углов равностороннего треугольника равна 180 градусов, поэтому каждый угол равностороннего треугольника равен 60 градусов.
Таким образом, в равнобедренном треугольнике с углом 40 градусов, оставшиеся два угла будут равны по 70 градусов каждый.
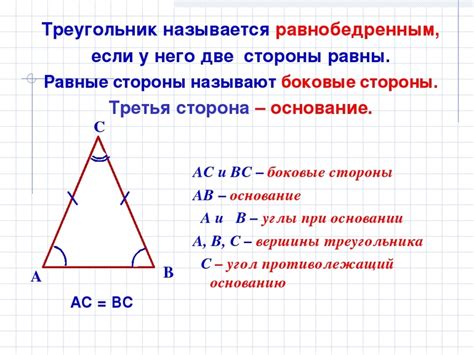
Что такое равнобедренный треугольник
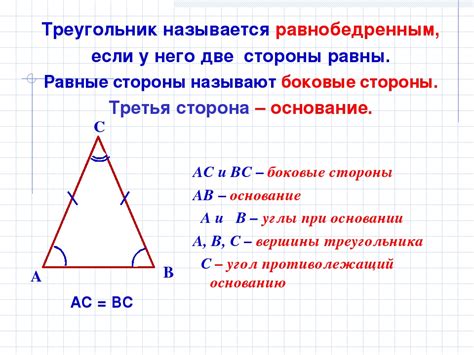
В равнобедренном треугольнике две стороны, называемые боковыми, имеют одинаковую длину, а третья сторона, называемая основанием, отличается от них. Углы при основании равнобедренного треугольника также равны, и часто обозначаются символом α.
Свойства равнобедренного треугольника
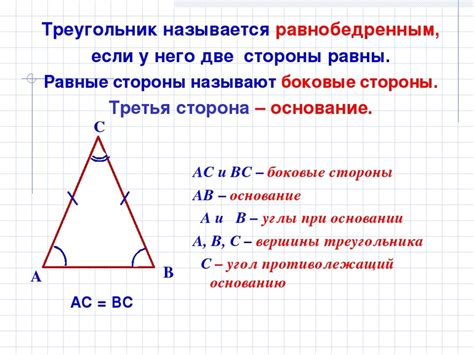
Основные свойства равнобедренного треугольника:
1) Углы при основании равны: В равнобедренном треугольнике углы при основании равны между собой. Если один из таких углов известен, то другой угол при основании также будет равен ему.
2) Боковые стороны равны: В равнобедренном треугольнике боковые стороны имеют одинаковую длину. Если длина одной из боковых сторон известна, то длина другой боковой стороны также будет равна ей.
3) Биссектриса угла при вершине делит основание на две равные части: Биссектриса угла при вершине равнобедренного треугольника делит основание на две равные части. То есть, от точки пересечения биссектрисы и основания до каждого конца основания расстояние будет одинаково.
Знание этих свойств помогает решать задачи по нахождению углов и длин сторон в равнобедренных треугольниках, а также решать другие математические задачи, связанные с равнобедренными треугольниками.
Как найти углы равнобедренного треугольника

Если известно, что угол вершины равен 40 градусам, то в равнобедренном треугольнике две другие углы также равны между собой.
Чтобы найти каждый из этих двух равных углов, нужно воспользоваться свойством суммы углов треугольника, сумма углов треугольника равна 180 градусам. В равнобедренном треугольнике один из углов равен 40 градусам. Таким образом, сумма двух меньших углов треугольника равна 180 градусам минус 40 градусов, что равно 140 градусам. Для того чтобы найти каждый из углов, нужно разделить эту сумму на 2, получив 70 градусов.
Итак, в равнобедренном треугольнике с углом вершины 40 градусов, оба других угла равны 70 градусам.
Угол основания и два угла при основании
Равнобедренный треугольник характеризуется наличием двух равных углов. Если один из них равен 40 градусам, то остальные углы также будут равны.
В равнобедренном треугольнике угол при основании, то есть угол, образованный двумя равными сторонами, всегда равен 180 минус два угла основания. Если один из углов основания равен 40 градусам, то второй угол основания будет также равен 40 градусам.
Таким образом, в равнобедренном треугольнике с углом 40 градусов, угол основания будет равен 180 - 40 - 40 = 100 градусам.
Два других угла треугольника, то есть углы при основании, будут равны 40 градусам каждый.
Таким образом, в равнобедренном треугольнике с углом 40 градусов, угол основания будет равен 100 градусам, а два других угла при основании будут равны 40 градусам каждый.
Синус угла равнобедренного треугольника
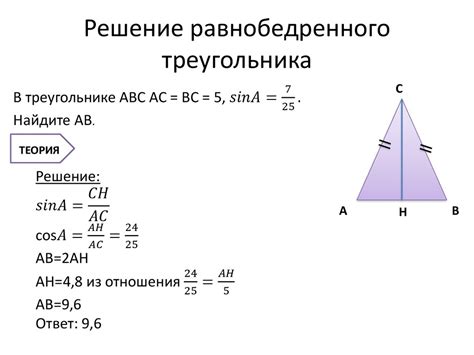
Синус угла равнобедренного треугольника может помочь вам в вычислениях, связанных с этим типом треугольников. В случае равнобедренного треугольника с углом 40 градусов, синус данного угла можно вычислить следующим образом:
sin(40 градусов) = длина основания / длина боковой стороны
Для дальнейших вычислений вам понадобятся значения длины основания и длины боковой стороны равнобедренного треугольника. Используя синус угла 40 градусов и известные значения, вы сможете рассчитать значения других углов равнобедренного треугольника.
Обратите внимание, что значение синуса угла равнобедренного треугольника всегда будет в пределах от 0 до 1.
Косинус угла равнобедренного треугольника
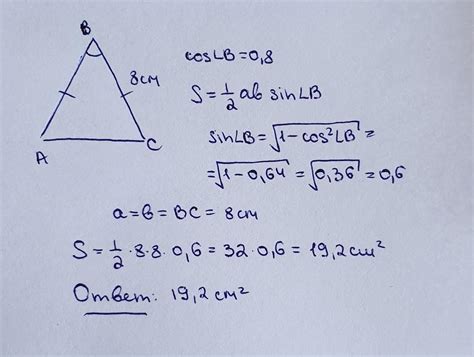
Для нахождения углов равнобедренного треугольника с углом 40 градусов необходимо использовать свойство косинуса.
Косинус угла в равнобедренном треугольнике можно найти, используя следующую формулу:
cos(половина угла) = (катет равнобедренного треугольника) / (гипотенуза треугольника)
Так как у равнобедренного треугольника два равных катета, то можно записать формулу для нахождения угла равнобедренного треугольника:
cos(половина угла) = (катет) / (гипотенуза треугольника)
Таким образом, для нахождения углов равнобедренного треугольника с углом 40 градусов необходимо:
1. Найти катет треугольника. Для этого можно воспользоваться теоремой косинусов, зная длины двух равных сторон и угол между ними.
2. Найти гипотенузу треугольника, которая также является стороной равнобедренного треугольника.
3. Подставить значения катета и гипотенузы в формулу для нахождения угла с помощью косинуса.
Таким образом, получаем значения углов равнобедренного треугольника с углом 40 градусов с использованием косинуса.
Тангенс угла равнобедренного треугольника

Углы равнобедренного треугольника имеют следующую характеристику: один угол равен 40 градусов, а два других угла составляют между собой равные значения.
Чтобы найти значения этих углов, можно использовать свойство тангенса.
Тангенс угла в прямоугольном треугольнике можно найти, разделив длину противоположной стороны на длину прилежащей стороны:
| Угол | Прилежащая сторона | Противоположная сторона | Тангенс угла |
|---|---|---|---|
| 40° | 1 | ? | ? |
| ? | ? | 1 | ? |
Так как два других угла равны, и противоположные им стороны также равны, то значения тангенса этих углов также будут равны:
| Тангенс угла | Значение |
| ? | ? |
Таким образом, для нахождения значений двух других углов равнобедренного треугольника можно использовать те же значения тангенса, что и для угла 40 градусов.
Примеры вычисления углов равнобедренного треугольника
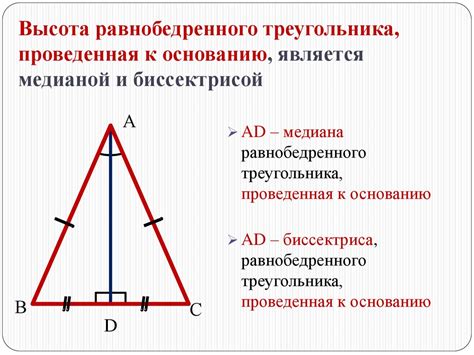
Угол 40 градусов делает треугольник равнобедренным, поскольку две его стороны будут равными. Давайте рассмотрим пример вычисления остальных углов такого треугольника.
- Вычислим угол между равными сторонами. Поскольку треугольник равнобедренный, угол между равными сторонами будет равным (180 - 40) / 2 = 70 градусов.
- Вычислим угол, образованный одной из равных сторон с основанием треугольника. Поскольку треугольник равнобедренный, этот угол будет равен (180 - 70) / 2 = 55 градусов.
Таким образом, углы равнобедренного треугольника с углом 40 градусов будут следующими:
- Угол между равными сторонами: 70 градусов.
- Угол между одной из равных сторон и основанием: 55 градусов.
- Угол между другой равной стороной и основанием: 55 градусов.
Пример 1: Длины сторон известны

Для нахождения углов равнобедренного треугольника, в котором один из углов равен 40 градусов, и известны длины его сторон, можно использовать теорему синусов. Теорема синусов позволяет вычислить значения углов треугольника, зная длины его сторон и противолежащие углы.
Для примера рассмотрим равнобедренный треугольник ABC, в котором угол BAC равен 40 градусов. Известны значения сторон AB, BC и AC.
- Задано значение угла BAC: 40 градусов.
- Известны значения сторон AB, BC и AC.
- Найдем противолежащий угол ABC.
- Используем теорему синусов: sin(BAC) / AC = sin(ABC) / AB.
- Подставляем известные значения: sin(40) / AC = sin(ABC) / AB.
- Находим значение sin(ABC) путем перемножения и деления: sin(ABC) = (AB * sin(40)) / AC.
- Используем обратную функцию синуса, чтобы найти значение угла ABC: ABC = arcsin((AB * sin(40)) / AC).
- Находим величину угла ABC, округляем до нужной степени.
- Угол ACB равен равен углу ABC, так как треугольник равнобедренный.
Таким образом, мы получили значения углов ABC и ACB равнобедренного треугольника с заданным углом BAC и известными длинами его сторон.
Пример 2: Известны угол при основании и угол между сторонами
Если в равнобедренном треугольнике известны угол при основании и угол между сторонами, то можно найти значения остальных двух углов.
Пусть углы при основании равны 40 градусов, а угол между сторонами равен 70 градусам.
Чтобы найти остальные два угла, вычтем из 180 градусов сумму угла при основании и угла между сторонами:
| Угол при основании (градусы) | Угол между сторонами (градусы) | Остальные два угла (градусы) |
|---|---|---|
| 40 | 70 | 70 |
Таким образом, остальные два угла равны 70 градусам каждый.
Итак, в равнобедренном треугольнике с углом при основании 40 градусов и углом между сторонами 70 градусов, все три угла равны 70 градусам.