Знание углов треугольника является необходимым для решения различных геометрических задач. Определение углов по сторонам треугольника является одной из таких задач. Это может быть полезно, когда известны длины сторон треугольника и требуется найти значения всех его углов.
Для решения этой задачи можно использовать теорему косинусов. Согласно этой теореме, квадрат длины одной из сторон треугольника равен сумме квадратов длин двух других сторон, умноженных на два произведения этих сторон и косинус угла между ними. Используя эту формулу, можно найти все углы треугольника.
Примером такой задачи может быть следующая ситуация: известны длины сторон треугольника, а также значение противолежащего угла. Для решения этой задачи мы можем использовать теорему синусов. По этой теореме, отношение синуса угла к длине противолежащей стороны для всех углов треугольника будет равным. Используя эту формулу, мы можем найти значения остальных углов треугольника.
Как найти углы треугольника по сторонам
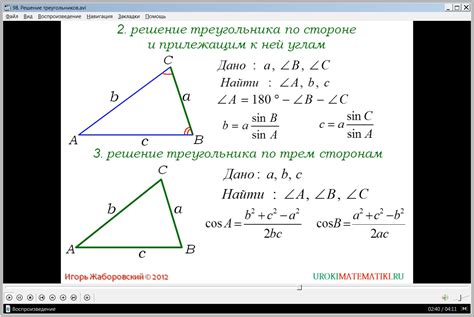
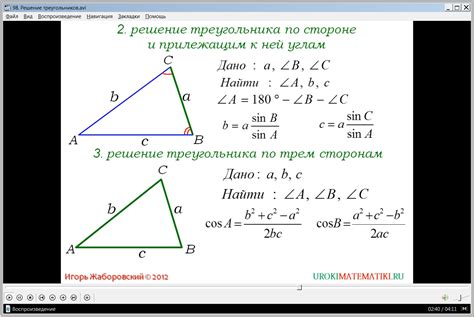
Для поиска углов треугольника по его сторонам существует несколько формул, основанных на теореме косинусов и теореме синусов. Эти формулы позволяют определить все углы треугольника, если известны длины трех его сторон.
Формула косинусов:
Для треугольника со сторонами А, В и С и противолежащими углами α, β и γ соответственно, формула косинусов выглядит следующим образом:
cos(α) = (B² + C² - A²) / (2 * B * C)
cos(β) = (A² + C² - B²) / (2 * A * C)
cos(γ) = (A² + B² - C²) / (2 * A * B)
Формула синусов:
Для треугольника со сторонами А, В и С и противолежащими углами α, β и γ соответственно, формула синусов имеет вид:
sin(α) = (B * sin(γ)) / A
sin(β) = (A * sin(γ)) / B
sin(γ) = (A * sin(α)) / C
Используя эти формулы, можно вычислить углы треугольника по длинам его сторон. Это особенно полезно, если известны только стороны треугольника и неизвестны его углы.
Формулы для нахождения углов треугольника
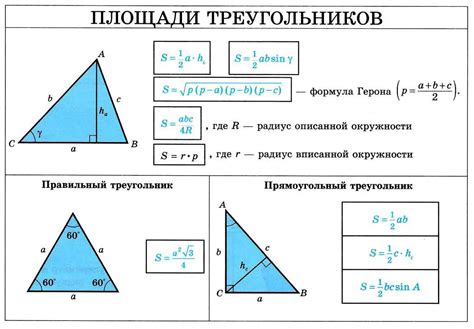
В геометрии существуют различные способы определить углы треугольника по его сторонам и противолежащему углу. Знание этих формул помогает нам решать задачи, связанные с треугольниками.
1. Формула синусов. Данная формула позволяет найти углы треугольника, если известны длины его сторон. Она выглядит следующим образом:
sinA = a / c, sinB = b / c, sinC = a / b
где A, B и C - углы треугольника, a, b и c - длины его сторон, причем a соответствует углу A, b - углу B и c - углу C.
2. Формула косинусов. Эта формула также используется для нахождения углов треугольника по его сторонам. Она имеет следующий вид:
cosA = (b^2 + c^2 - a^2) / (2 * b * c), cosB = (a^2 + c^2 - b^2) / (2 * a * c), cosC = (a^2 + b^2 - c^2) / (2 * a * b)
3. Формула тангенсов. Эта формула позволяет найти углы треугольника, используя длины его сторон:
tgA = (2 * p * r) / (q^2 - r^2), tgB = (2 * q * r) / (p^2 - r^2), tgC = (2 * p * q) / (p^2 + q^2)
где p, q и r - полупериметр и радиус вписанной окружности треугольника соответственно.
Зная эти формулы, мы можем находить углы треугольника, используя данные о его сторонах и противолежащему угле. Решая задачи, связанные с треугольниками, необходимо быть внимательным и не допускать ошибок при подстановке значений.
Пример нахождения углов треугольника по сторонам
Допустим, у нас есть треугольник ABC, у которого известны значения сторон a, b и c:
| Сторона | Значение |
|---|---|
| AB | a |
| BC | b |
| AC | c |
Чтобы найти значения углов треугольника, можно использовать "Закон косинусов" и "Закон синусов".
1. Найдем угол A, противолежащий стороне a:
Используя "Закон косинусов", мы можем выразить косинус угла A:
cos(A) = (b^2 + c^2 - a^2) / (2 * b * c)
Используя обратную функцию косинуса, мы можем найти значение угла A:
A = arccos((b^2 + c^2 - a^2) / (2 * b * c))
2. Найдем угол B, противолежащий стороне b:
Используя "Закон косинусов", мы можем выразить косинус угла B:
cos(B) = (a^2 + c^2 - b^2) / (2 * a * c)
Используя обратную функцию косинуса, мы можем найти значение угла B:
B = arccos((a^2 + c^2 - b^2) / (2 * a * c))
3. Угол C может быть найден, используя сумму углов треугольника:
C = 180 - A - B
Таким образом, мы можем найти значения всех углов треугольника по значениям его сторон.
Как найти противолежащий угол треугольника
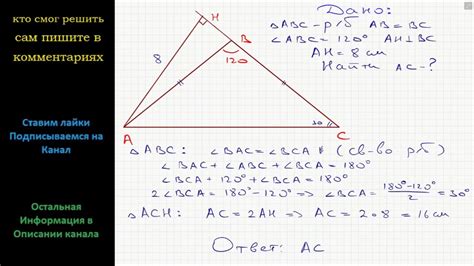
Если известны длины всех сторон треугольника, противолежащий угол можно найти с помощью закона косинусов. Формула для вычисления противолежащего угла треугольника выглядит следующим образом:
cos(A) = (b^2 + c^2 - a^2) / (2bc)
где A – противолежащий угол, a, b и c – длины сторон треугольника.
Если известны длины двух сторон треугольника и значение угла между ними, противолежащий угол можно найти с помощью закона синусов. Формула вычисления противолежащего угла с использованием закона синусов выглядит следующим образом:
sin(A) = (a / c) * sin(B)
где A – противолежащий угол, a – длина одной из смежных сторон, c – длина третьей стороны, B – значение угла между известными сторонами.
Зная значения сторон и углов треугольника, можно использовать эти формулы для нахождения противолежащего угла. Это может быть полезно, например, при решении геометрических задач или для определения характеристик треугольника.
Формула для нахождения противолежащего угла треугольника
При известных длинах сторон треугольника a, b, c можно использовать формулу для нахождения противолежащего угла треугольника. Для этого необходимо знать значения всех сторон треугольника.
Формула для вычисления противолежащего угла треугольника может выглядеть следующим образом:
cos(A) = (b^2 + c^2 - a^2) / (2 * b * c)
Здесь A обозначает противолежащий угол, a - сторону, противолежащую углу A, b и c - оставшиеся две стороны треугольника. Косинус угла A можно найти, решив данное уравнение.
После нахождения значения cos(A), можно использовать функцию арккосинуса, чтобы найти искомый угол A. Формула будет выглядеть так:
A = arccos(cos(A))
Таким образом, применяя данные формулы, можно вычислить противолежащий угол треугольника при известных сторонах.
Пример нахождения противолежащего угла треугольника

Рассмотрим треугольник ABC, где стороны треугольника обозначены как a, b и c, а противолежащий угол треугольника обозначен как угол А. Для нахождения значения угла А с использованием сторон треугольника, мы можем воспользоваться теоремой косинусов.
Теорема косинусов гласит:
Квадрат стороны треугольника a равен сумме квадратов сторон b и c, уменьшенной на произведение сторон b и c и косинуса угла А:
a2 = b2 + c2 - 2bc * cos(A)
Чтобы найти угол А, мы можем перенести член с косинусом на другую сторону уравнения и взять арккосинус от полученной формулы:
A = arccos((b2 + c2 - a2) / (2bc))
Давайте рассмотрим конкретный пример. Пусть у нас есть треугольник ABC, где стороны равны a = 5, b = 4 и c = 6. Найдем противолежащий угол А.
| Сторона | Значение |
|---|---|
| a | 5 |
| b | 4 |
| c | 6 |
Используя формулу для нахождения противолежащего угла, получаем:
A = arccos((42 + 62 - 52) / (2 * 4 * 6))
Вычисляя это выражение, получаем:
A ≈ arccos(37 / 48) ≈ 0.7754 радиан ≈ 44.4 градусов
Таким образом, противолежащий угол А примерно равен 44.4 градусов для треугольника со сторонами 5, 4 и 6.