Найти углы треугольника по сторонам и углу между ними - это важный навык при решении геометрических задач. Мы часто сталкиваемся с треугольниками в повседневной жизни, и знание, как вычислить углы этой фигуры, может быть полезно. Существует несколько способов решения этой задачи, и мы рассмотрим их подробно.
Один из самых простых способов найти углы треугольника - использовать теорему косинусов. Эта теорема гласит, что квадрат одной стороны треугольника равен сумме квадратов двух других сторон, умноженных на косинус угла между ними. Используя эту теорему, можно найти углы треугольника, если известны все его стороны.
Еще один способ найти углы треугольника - использовать теорему синусов. Эта теорема гласит, что отношение синуса угла треугольника к длине противоположной стороны равно отношению синуса угла к длине противоположной стороны. Для нахождения углов треугольника можно использовать эту теорему, если известны длины двух сторон и угол между ними.
Используя эти методы и зная несколько простых формул, можно легко найти углы треугольника по сторонам и углу между ними. Эти знания пригодятся не только в математических задачах, но и в повседневной жизни, помогая решать различные геометрические задачи.
Формула косинусов для нахождения углов треугольника
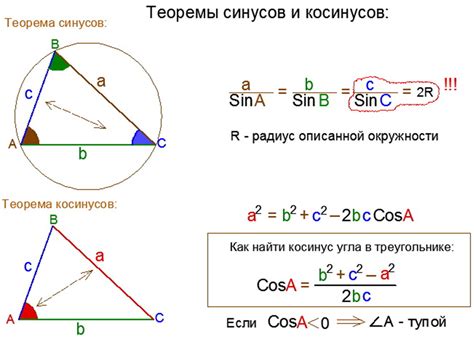
Если известны длины всех трех сторон треугольника - a, b и c, и угол между сторонами a и b - C, то можно использовать формулу косинусов для нахождения меры каждого из трех углов треугольника.
Формула косинусов имеет вид:
cos(A) = (b^2 + c^2 - a^2) / (2 * b * c)
cos(B) = (a^2 + c^2 - b^2) / (2 * a * c)
cos(C) = (a^2 + b^2 - c^2) / (2 * a * b)
Где A, B и C - меры углов треугольника, a, b и c - длины сторон треугольника.
Используя эти формулы, можно вычислить значение каждого из углов треугольника, если известны длины всех его сторон и мера угла между ними.
Использование теоремы синусов для определения углов треугольника
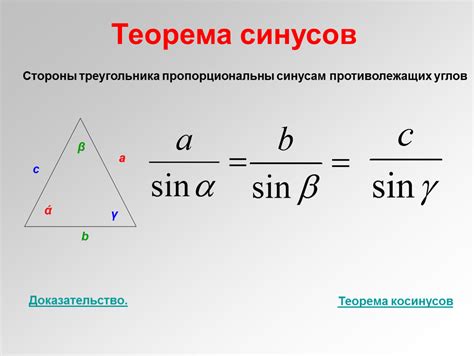
Формула теоремы синусов имеет следующий вид:
| a | / | sin ∠A |
| b | / | sin ∠B |
| c | / | sin ∠C |
Где a, b и c - длины сторон треугольника, а ∠A, ∠B и ∠C - соответствующие углы.
Чтобы определить углы треугольника с помощью теоремы синусов, мы должны знать длины всех трех его сторон и угол, расположенный между ними. После подстановки известных значений в формулу, мы можем выразить каждый угол треугольника через соответствующий синус. Затем, используя обратные функции синуса, мы можем найти численные значения углов.
Теорема синусов является совершенным инструментом для решения различных задач по треугольникам. Она позволяет нам определить углы треугольника, используя только информацию о его сторонах и угле между ними.
Теперь, с помощью этой формулы, вы можете легко определить углы вашего треугольника, если у вас есть все необходимые данные. Удачи в изучении геометрии!
Применение тригонометрических функций для нахождения углов треугольника
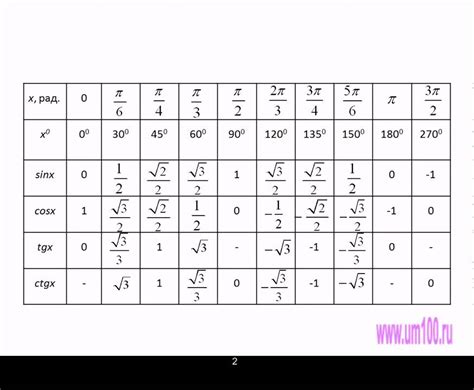
Тригонометрические функции широко применяются для нахождения углов треугольника по известным сторонам и углу между ними. Знание этих функций позволяет решать сложные геометрические задачи и выполнять точные расчеты.
Самые часто используемые тригонометрические функции - синус (sin), косинус (cos) и тангенс (tg). Они определены отношениями сторон треугольника и позволяют найти значения углов. Все эти функции можно вычислить с помощью калькулятора или специальных таблиц.
Для нахождения углов треугольника с помощью тригонометрических функций необходимо знать длины сторон треугольника и угол между ними. Воспользуемся следующими формулами:
Для нахождения угла A:
sin(A) = (a / c)
cos(A) = (b / c)
tg(A) = (a / b)
Для нахождения угла B:
sin(B) = (b / c)
cos(B) = (a / c)
tg(B) = (b / a)
Для нахождения угла C:
sin(C) = (a / b)
cos(C) = (c / b)
tg(C) = (a / c)
После нахождения значений тригонометрических функций можно найти значения углов при помощи обратных функций arcsin, arccos и arctg. Таким образом, нахождение углов треугольника становится возможным с использованием тригонометрии.
Важно помнить, что для использования этих формул необходимо, чтобы стороны треугольника были известны и соответствующие углы находились между ними. В противном случае, эти формулы не будут применимы.
Расчет углов треугольника с использованием длин сторон и угла между ними
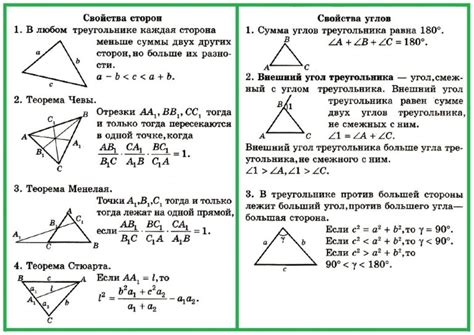
Углы треугольника могут быть рассчитаны с использованием длин сторон и угла между ними. Для этого можно использовать законы синусов и косинусов.
Закон синусов утверждает, что отношение каждой стороны треугольника к синусу противолежащего ей угла является постоянным. То есть:
sin(A) / a = sin(B) / b = sin(C) / c
где A, B и C - углы треугольника, а a, b и c - длины соответствующих сторон.
Для нахождения отдельных углов можно использовать обратную функцию синуса (arcsin) или тригонометрическую функцию arccos (арккосинус).
Например, если заданы длины сторон a = 4, b = 5 и c = 6, а угол A равен 30 градусам, то можно воспользоваться формулой:
A = arcsin((a * sin(B)) / b)
Для нашего примера:
A = arcsin((4 * sin(30)) / 5)
Подставив значения в формулу и рассчитав, получим:
A ≈ 34.5 градусов
Аналогичным образом можно рассчитать углы B и C.
Таким образом, для расчета углов треугольника с использованием длин сторон и угла между ними, необходимо знать длины всех сторон и значение одного из углов. Затем, используя закон синусов или косинусов, можно рассчитать остальные углы при помощи математических формул и функций.
Дополнительные методы определения углов треугольника
Не всегда у нас есть доступ к данным о сторонах и углах треугольника. В некоторых случаях мы можем столкнуться с ситуацией, когда нам известны только некоторые из этих параметров. В таких случаях нам потребуются дополнительные методы для определения углов треугольника.
Один из таких методов - использование свойства суммы углов треугольника. Все углы треугольника в сумме дают 180 градусов. Если мы знаем два угла треугольника, мы можем вычислить третий угол, вычитая сумму этих двух углов из 180 градусов.
Еще один метод - использование тригонометрических функций. Если мы знаем длины двух сторон треугольника и угол между ними, мы можем использовать косинусную или синусную теорему для вычисления третьего угла. Косинусная теорема гласит, что квадрат длины стороны треугольника равен сумме квадратов длин двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними. Синусная теорема гласит, что отношение длины стороны к синусу угла напротив этой стороны равно отношению длин двух других сторон к синусам соответствующих им углов.
Если у нас есть информация о высоте треугольника и основании, мы можем использовать теорему Пифагора для вычисления углов треугольника. Теорема Пифагора гласит, что квадрат длины гипотенузы треугольника равен сумме квадратов длин двух других его сторон. Мы можем использовать эту теорему для вычисления одного из углов треугольника, если мы знаем длины всех его сторон.
Зная длины трех сторон треугольника, мы можем использовать теорему косинусов для вычисления углов. Теорема косинусов утверждает, что косинус угла треугольника равен сумме квадратов длин двух других его сторон минус удвоенное произведение этих сторон на косинус угла между ними, деленное на произведение длин этих сторон.
Важные моменты при расчете углов треугольника
При расчете углов треугольника по сторонам и углу между ними необходимо учитывать несколько важных моментов. Вот некоторые из них:
1. Тригонометрические функции: Для расчета углов треугольника можно использовать тригонометрические функции, такие как синус, косинус и тангенс. Для этого необходимо знать значения сторон и угла между ними.
2. Законы синусов и косинусов: Для треугольников произвольной формы существуют законы, позволяющие выразить углы через стороны и углы между ними. Закон синусов позволяет определить отношение сторон к синусу соответствующих углов, а закон косинусов - выразить косинус угла через стороны треугольника.
3. Сумма углов треугольника: В любом треугольнике сумма углов равна 180 градусов. Это позволяет использовать эту информацию для нахождения неизвестных углов при известных углах или нахождении третьего угла при известных двух углах.
4. Использование теоремы косинусов: Если известны длины всех трех сторон треугольника, то можно воспользоваться теоремой косинусов. Она позволяет выразить косинус угла через длины сторон треугольника и наоборот. Это может быть полезно для определения углов, когда известны лишь стороны.
5. Учет особенностей задачи: При расчете углов треугольника необходимо учитывать особенности задачи, такие как наличие прямого угла, равенство сторон или углов, соотношение между сторонами и другие условия.
Учитывая эти важные моменты, можно эффективно находить углы треугольника по сторонам и углу между ними.