Предположим, вы знаете длины всех трех сторон треугольника, но вам необходимо найти значения его углов. Поиск углов треугольника по сторонам может быть сложной задачей, но с правильным подходом это становится возможным. В данной статье мы рассмотрим детальные инструкции, которые помогут вам узнать углы треугольника на основе заданных сторон.
Первый шаг – применить теорему косинусов. Эта теорема позволяет находить углы треугольника, зная длины его сторон. Формула выглядит следующим образом: c^2 = a^2 + b^2 - 2ab * cos(C), где c – длина противолежащей стороны, a и b – длины двух других сторон, а C – искомый угол. Для нахождения значения угла C можно использовать обратный косинус (арккосинус) функции в программе или калькуляторе.
Когда вы найдете один угол треугольника, вы можете найти остальные два, используя остаточные свойства треугольника. Сумма значений всех углов треугольника всегда равна 180 градусам. Зная один угол треугольника, вы можете найти второй, вычитая это значение из 180 градусов. Затем, для нахождения третьего угла просто вычитаете значение первого и второго угла из 180°.
Теперь вы знаете, как найти углы треугольника по заданным сторонам. Используйте эти инструкции для решения геометрических задач и расчетов в будущем. Помните, что для более сложных и нестандартных треугольников может потребоваться использование других формул и методов, но основные принципы останутся прежними.
Как найти углы треугольника по сторонам: Подробная инструкция
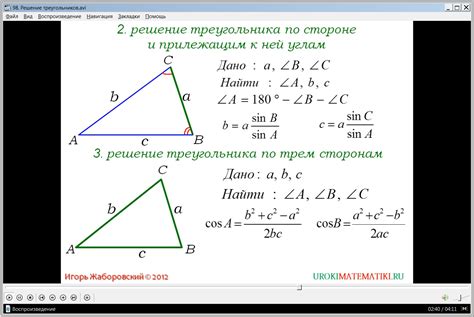
Если у вас есть треугольник, но отсутствуют его углы, вы можете найти их, зная длины сторон. Следуя этой подробной инструкции, вы сможете точно вычислить углы треугольника.
Шаг 1: Возьмите треугольник и обозначьте его стороны a, b и c. Здесь a - наибольшая сторона, b и c - остальные две стороны.
Шаг 2: Используя теорему косинусов, выразите один из углов треугольника через длины его сторон. Формула следующая:
cos(A) = (b^2 + c^2 - a^2) / 2bc
где A - угол противоположный стороне a.
Шаг 3: Используя эту формулу, найдите значение cos(A) и найдите угол A с помощью инверсного косинуса:
A = arccos((b^2 + c^2 - a^2) / 2bc)
Шаг 4: Повторите шаги 2 и 3 для каждого из двух оставшихся углов треугольника. Используйте соответствующие формулы для каждого угла, заменяя соответствующие переменные.
Шаг 5: Проверьте результаты, убедившись, что сумма всех трех углов равна 180 градусам. Если это так, значит вы правильно вычислили углы треугольника.
Следуя этой подробной инструкции, вы сможете легко найти углы треугольника, зная только длины его сторон. Помните, что этот метод основан на теореме косинусов и может быть использован только для неравнобедренных треугольников.
Что такое треугольник и какие у него стороны?

У треугольника есть три стороны: AB, BC и AC. Сторона AB соединяет вершины A и B, сторона BC - вершины B и C, а сторона AC - вершины A и C. Величины сторон треугольника могут быть различными и обозначаются разными буквами или символами.
Строение треугольника определяется длинами его сторон и величинами его углов. В зависимости от длин сторон треугольники могут быть разделены на различные виды: равносторонний (все стороны равны), равнобедренный (две стороны равны), разносторонний (все стороны различны).
Изучение треугольников и его сторон позволяет решать различные геометрические задачи, включая определение углов треугольника по известным сторонам.
Формула для вычисления углов треугольника по сторонам
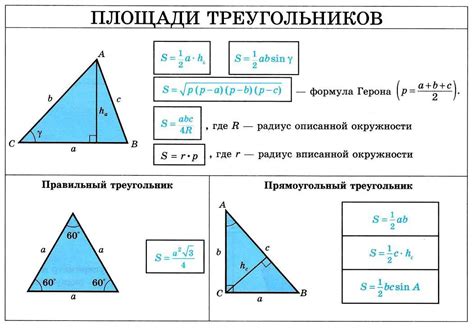
Для вычисления углов треугольника по известным сторонам применяется формула, известная как теорема косинусов. Эта формула позволяет определить все три угла треугольника, если известны длины его сторон.
Формула выглядит следующим образом:
| cos(A) = | (b^2 + c^2 - a^2) / (2 * b * c) |
| cos(B) = | (a^2 + c^2 - b^2) / (2 * a * c) |
| cos(C) = | (a^2 + b^2 - c^2) / (2 * a * b) |
Где A, B, C - углы треугольника, a, b, c - длины его сторон.
Чтобы найти углы треугольника, необходимо использовать обратную функцию косинуса (арккосинус) для нахождения значения угла, основываясь на значениях полученных косинусов.
Например:
A = arccos(cos(A)) B = arccos(cos(B)) C = arccos(cos(C))
Важно помнить, что результаты углов будут выражены в радианах. Для перевода в градусы необходимо умножить их на (180/π).
Таким образом, с использованием теоремы косинусов и обратной функции косинуса, можно найти углы треугольника по известным сторонам.