Треугольник – это одна из самых простых и в то же время увлекательных геометрических фигур. У него есть три стороны и три угла. Обычно, нам известны исходные значения сторон, и мы хотим узнать, какие углы образуют этот треугольник. В этой статье мы рассмотрим, как решить эту задачу с использованием языка программирования Python.

Для решения этой задачи мы можем использовать закон косинусов, который утверждает, что квадрат длины одной стороны треугольника равен сумме квадратов длин двух других сторон, умноженных на два произведения этих сторон и косинуса между ними. Используя этот закон, мы можем выразить косинус одного из углов треугольника и вычислить его значение.

Для вычисления косинуса угла в Python существует функция math.cos(). Мы можем использовать эту функцию, чтобы найти значение косинуса угла. Затем, используя функцию math.acos(), мы можем вычислить обратный косинус и получить значение угла в радианах.

Как определить углы треугольника в питоне?

Для определения углов треугольника по трём сторонам в питоне можно использовать теорему косинусов и функции из стандартной библиотеки math.

1. Импортируйте модуль math:

import math

2. Задайте длины сторон треугольника:

a = 3
b = 4
c = 5

3. Вычислите косинусы углов при помощи теоремы косинусов:

cos_a = (b**2 + c**2 - a**2) / (2 * b * c)
cos_b = (c**2 + a**2 - b**2) / (2 * c * a)
cos_c = (a**2 + b**2 - c**2) / (2 * a * b)

4. Преобразуйте косинусы в углы, используя функцию math.acos:

angle_a = math.degrees(math.acos(cos_a))
angle_b = math.degrees(math.acos(cos_b))
angle_c = math.degrees(math.acos(cos_c))

Теперь переменные angle_a, angle_b, angle_c содержат значения углов треугольника в градусах.

Можно использовать эти значения для анализа и дальнейших вычислений, например, для проверки типа треугольника (остроугольный, тупоугольный, прямоугольный) или для нахождения других характеристик треугольника.

Основные принципы нахождения углов треугольника по известным сторонам

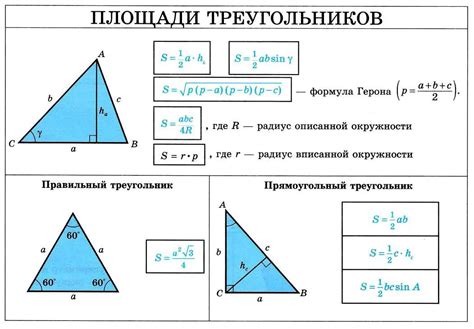
Когда известны длины всех трех сторон треугольника, можно найти все его углы, используя формулы косинусов и теорему косинусов.

Формулы косинусов применяются для нахождения конкретного угла треугольника и выглядят следующим образом:

cos(A) = (b^2 + c^2 - a^2) / (2bc)

cos(B) = (a^2 + c^2 - b^2) / (2ac)

cos(C) = (a^2 + b^2 - c^2) / (2ab)

Где A, B, C - углы треугольника, a, b, c - его стороны.

Теорема косинусов устанавливает связь между длинами сторон треугольника и косинусами его углов:

a^2 = b^2 + c^2 - 2bc * cos(A)

b^2 = a^2 + c^2 - 2ac * cos(B)

c^2 = a^2 + b^2 - 2ab * cos(C)

Используя данные формулы, можно вычислить углы треугольника по известным сторонам с помощью языка программирования Python.

Метод 1: Использование теоремы косинусов

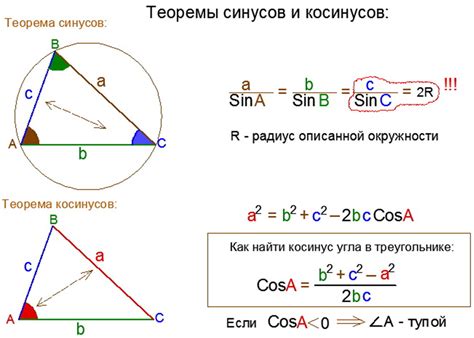
Для нахождения углов треугольника по заданным сторонам можно воспользоваться теоремой косинусов, которая устанавливает связь между длинами сторон треугольника и значением его углов.

Теорема косинусов гласит:

• Для стороны A против угла α: A² = B² + C² - 2BC ⋅ cosα
• Для стороны B против угла β: B² = A² + C² - 2AC ⋅ cosβ
• Для стороны C против угла γ: C² = A² + B² - 2AB ⋅ cosγ

Используя эти формулы, можно выразить косинусы углов треугольника:

• cosα = (B² + C² - A²) / (2BC)
• cosβ = (A² + C² - B²) / (2AC)
• cosγ = (A² + B² - C²) / (2AB)

Зная косинусы углов, можно найти значения самих углов с помощью функции арккосинуса (math.acos) и перевести полученные значения из радиан в градусы.

Метод 2: Использование теоремы синусов

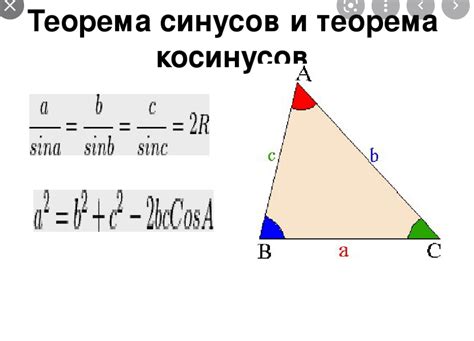
Треугольник может быть решен, используя теорему синусов. Теорема синусов утверждает, что отношение синуса угла к длине противолежащей стороны для всех трех углов треугольника одинаковы.

Для нахождения углов треугольника по трем сторонам, нужно следовать следующим шагам:

1. Найти длину каждой стороны треугольника.
2. Найти синус каждого угла, используя формулу sin(A) = a / c, где A - угол, a - противолежащая сторона и с - гипотенуза треугольника.
3. Используя формулу sin^(-1) (обратный синус), найти значение каждого угла, где sin^(-1) - обратный синус функции.

Приведенный ниже код на Python демонстрирует, как реализовать этот метод:

import math
def find_angles(side1, side2, side3):
# Используем закон синусов, чтобы найти углы треугольника
angle1 = math.degrees(math.asin(side1 / side3))
angle2 = math.degrees(math.asin(side2 / side3))
angle3 = 180 - angle1 - angle2
return angle1, angle2, angle3

Вы можете вызвать эту функцию с длиной каждой стороны треугольника и она вернет значения углов треугольника:

angle1, angle2, angle3 = find_angles(5, 7, 8)
print("Угол 1:", angle1)
print("Угол 2:", angle2)
print("Угол 3:", angle3)

В результате выполнения кода будут выведены значения углов треугольника:

Угол 1: 36.86989764584402
Угол 2: 53.13010235415599
Угол 3: 90.0

Теперь у вас есть метод, который позволяет найти углы треугольника, используя длины его сторон.