Углы их фигуры - это одна из самых фундаментальных и важных концепций в геометрии. Они используются почти во всех областях науки и техники, включая физику, инженерию, геодезию и другие. Познание правил и методов нахождения углов особенно полезно при работе с прямоугольными треугольниками, где один из углов равен 90 градусам.
Тангенс - это одно из основных тригонометрических отношений, которое позволяет нам вычислять углы на основе отношения длин противоположной и прилежащей сторон прямоугольного треугольника. Если у нас есть информация о противоположной и прилежащей сторонах треугольника, мы можем использовать формулу тангенса, чтобы найти величину угла. Формула выглядит следующим образом: тангенс угла (T) равен отношению противоположной стороны (O) к прилежащей стороне (A): T = O / A.
Давайте рассмотрим пример, чтобы лучше понять, как найти угол по тангенсу в прямоугольном треугольнике. Предположим, у нас есть треугольник, в котором длина противоположной стороны равна 5, а длина прилежащей стороны равна 3. Чтобы найти угол, мы можем использовать формулу тангенса: T = O / A. Подставляя значения, получим T = 5 / 3. Значение тангенса можно найти с помощью калькулятора или таблицы тангенсов. Найденное значение тангенса равно примерно 1,67. Заключительный этап - нахождение угла по значению тангенса с использованием обратной функции тангенса (arctan). В нашем примере полученный угол будет примерно равен 59,04 градусам.
Что такое угол по тангенсу
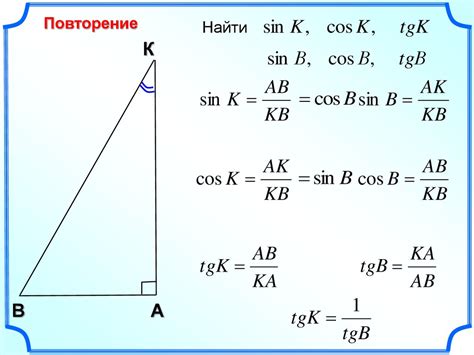
Формула для вычисления угла по тангенсу:
угол = arctan(тангенс)
Пример:
Допустим, что нам известно значение тангенса угла и мы хотим найти значение самого угла. Если тангенс угла равен 0.577, то мы можем вычислить угол по формуле: угол = arctan(0.577). Результатом будет приблизительно 30 градусов.
Угол по тангенсу является важным понятием в треугольной геометрии. Он позволяет нам находить углы, используя только значения тангенса и обратной функции - арктангенса. Это особенно полезно при работе с прямоугольными треугольниками и решении задач, связанных с измерением углов.
Определение и смысл

Тангенс угла является основной тригонометрической функцией, которая возвращает отношение противолежащего катета к прилежащему катету. В прямоугольном треугольнике это отношение полезно для определения угла, если известны значения этих катетов.
| Тангенс угла | Значение отношения | Угол |
|---|---|---|
| tan(30°) | 1 / √3 | 30° |
| tan(45°) | 1 | 45° |
| tan(60°) | √3 | 60° |
Зная значение тангенса угла, можно использовать формулы для нахождения самого угла. Например, чтобы найти угол по тангенсу 1/2, мы можем использовать арктангенс, который возвращает угол, значение тангенса которого равно данному. В данном случае, арктангенс 1/2 равен примерно 26.57°.
Углы в прямоугольных треугольниках играют важную роль при решении задач в различных областях, таких как физика, геометрия и инженерия. Знание тангенса угла и умение находить углы по тангенсу помогает улучшить точность вычислений и решить разнообразные задачи.
Формула вычисления
Для вычисления угла по тангенсу в прямоугольном треугольнике можно использовать основную тангенсовую формулу:
tg(α) = противолежащая сторона / прилежащая сторона
где α - искомый угол, противолежащая сторона - длина стороны, лежащей напротив угла α, и прилежащая сторона - длина стороны, лежащей рядом с углом α.
Для вычисления угла α нужно взять обратный тангенс (арктангенс) от отношения противолежащей стороны к прилежащей стороне:
α = arctg(противолежащая сторона / прилежащая сторона)
Например, если противолежащая сторона равна 3, а прилежащая сторона равна 4, то:
α = arctg(3/4) ≈ 36.87°
Таким образом, искомый угол α составляет примерно 36.87 градусов.
Тангенс и его свойства
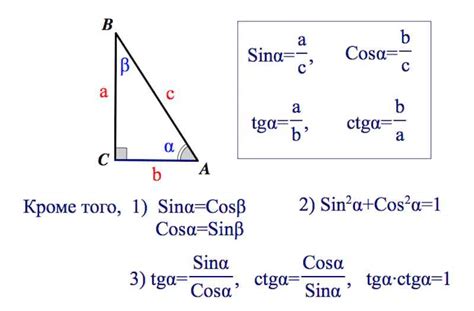
Тангенс имеет несколько свойств:
| Свойство | Формула |
|---|---|
| Ограничения значения | tg(θ) определен только при θ ≠ 90° + k180°, где k - любое целое число |
| Периодичность | tg(θ) периодична с периодом 180° (tg(θ) = tg(θ + k180°), где k - любое целое число) |
| Асимптотическое поведение | tg(θ) при θ → 90° или θ → –90° стремится к бесконечности |
| Отношение к другим тригонометрическим функциям | tg(θ) = sin(θ) / cos(θ) |
Зная значение тангенса, можно найти угол в прямоугольном треугольнике, используя обратную функцию - арктангенс (atan или arctan). По формуле θ = arctan(tg(θ)), можно определить угол противолежащий катет которого является известным.
Примеры решения

Рассмотрим несколько примеров, чтобы понять, как можно найти угол по тангенсу.
Пример 1:
- Дано: тангенс угла равен 0,5.
- Решение:
- Используя теорему Пифагора, найдем длины катетов:
- Пусть катеты равны 1 и x.
- Используя формулу для тангенса, получим: 0,5 = 1 / x.
- Решая данное уравнение, получим x = 2.
- Теперь можно найти значения синуса и косинуса с помощью найденных катетов и гипотенузы:
- Синус угла равен противолежащему катету (1) / гипотенузе (2), то есть 1 / 2, или 0.5.
- Косинус угла равен прилежащему катету (1) / гипотенузе (2), то есть 1 / 2, или 0.5.
Пример 2:
- Дано: тангенс угла равен 1.
- Решение:
- Используя теорему Пифагора, найдем длины катетов:
- Пусть катеты равны 1 и x.
- Используя формулу для тангенса, получим: 1 = 1 / x.
- Решая данное уравнение, получим x = 1.
- Теперь можно найти значения синуса и косинуса с помощью найденных катетов и гипотенузы:
- Синус угла равен противолежащему катету (1) / гипотенузе (1), то есть 1 / 1, или 1.
- Косинус угла равен прилежащему катету (1) / гипотенузе (1), то есть 1 / 1, или 1.
Таким образом, приведенные примеры демонстрируют, как можно решить уравнение для нахождения угла по заданному значению тангенса в прямоугольном треугольнике.
Практическое применение

Знание способов нахождения угла по тангенсу в прямоугольном треугольнике может быть полезным в различных практических ситуациях. Например:
- Строительство: при проектировании зданий и сооружений необходимо учитывать углы наклона и наклонные отрезки. При использовании треугольников и известных значений тангенса возможно рассчитать углы наклона скатов крыши или наклон дороги.
- Навигация: в морской и воздушной навигации тангенс используется для определения угла между направлением движения и линией, соединяющей две точки. Это помогает пилотам и навигаторам правильно установить курс и избежать коллизий с другими объектами.
- Инженерные расчеты: при проектировании мостов, дамб, трубопроводов и других инженерных сооружений необходимо учитывать нагрузки и наклоны. Зная значения тангенса, можно рассчитать углы наклона конструкций и определить необходимую прочность материалов.
- Физика и математика: в решении задач и формулах, связанных с тригонометрией, углами и расчетами, нахождение угла по тангенсу может быть необходимым шагом.
Все эти примеры показывают, что знание и умение применять формулы нахождения угла по тангенсу в прямоугольном треугольнике является полезным и полезным навыком в различных областях.
Отличия от других тригонометрических функций
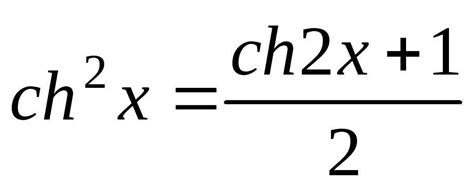
Тангенс угла в прямоугольном треугольнике определяется как отношение противоположной стороны треугольника к прилежащей стороне. Формула для нахождения тангенса угла выглядит следующим образом: тангенс угла = противоположная сторона / прилежащая сторона.
В отличие от синуса и косинуса, которые могут принимать значения от -1 до 1, тангенс угла может быть любым числом. Это связано с тем, что тангенс определен как отношение двух сторон и не ограничивается конкретным диапазоном значений. Это делает тангенс более универсальной функцией в сравнении с синусом и косинусом.
Однако, стоит отметить, что тангенс может быть бесконечным, если прилежащая сторона приближается к нулю. Это означает, что если угол прямоугольного треугольника прилежащий к стороне становится очень близким к 90 градусам, то тангенс этого угла будет стремиться к бесконечности.
Эти отличия делают тангенс уникальной тригонометрической функцией, которая имеет свои особенности и применение при решении задач связанных с прямоугольными треугольниками.
Сводная таблица значений
Ниже приведена сводная таблица значений для нахождения углов по тангенсу в прямоугольном треугольнике.
Угол (в градусах)
Тангенс
0°
0
15°
0.268
30°
0.577
45°
1
60°
1.732
75°
3.732
90°
Инфинити
Используя значения тангенса из этой таблицы, вы можете легко найти углы в прямоугольном треугольнике, при условии, что вам известно значение тангенса для одного из углов.